题目内容
【题目】如图,五边形ABCDE的内角都相等,且AB=BC,AC=AD,求∠CAD的度数.
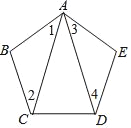
【答案】∠CAD=36°.
【解析】
根据多边形的内角和公式先求出每个内角的度数,再根据已知和三角形内角和等于180分别求出∠1、∠2的度数,从而得到∠ACD与∠ADC的度数,最后由三角形内角和定理求出∠CAD度数.
解:∵五边形ABCDE的内角都相等,
∴∠BAE=∠B=∠BCD=∠CDE=∠E=(5﹣2)×180°÷5=108°,
∵AB=AC,
∴∠1=∠2=(180°﹣108°)÷2=36°,
∴∠ACD=∠BCD﹣∠2=72°,
∵AC=AD,
∴∠ADC=∠ACD=72°,
∴∠CAD=180°﹣∠ACD﹣∠ADC=36°.
故答案为:36°.

练习册系列答案
相关题目