��Ŀ����
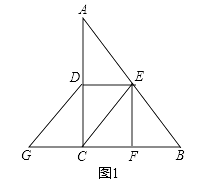
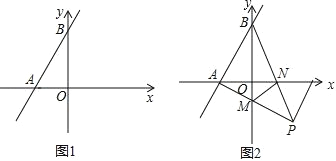
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ�� AB �ֱ� x �ᡢy ���ڵ�A��a��0���� B��0��b������a��b����a2+4a+4+|2a+b|��0
��1��a�� ��b�� ��
��2���� P ��ֱ��AB���Ҳ࣬����APB��45��
������P��x���ϣ����P������Ϊ ��
������ABP Ϊֱ�������Σ����P�����ꣻ
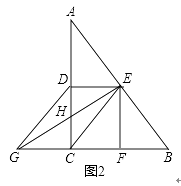
��2����ͼ2���ڣ�2���������£���P�ڵ������ޣ���BAP��90�㣬AP��y�ύ�ڵ�M��BP��x�ύ�ڵ�N������MN����֤��MPƽ����BMN��һ����ǣ�
���𰸡���1����2��4����2���٣�4��0������P��4��2����2����2������3���������.
��������
��1�����÷Ǹ����ĺ͵���0�����ɽ������������a��b��
��2�������õ���ֱ�������ε����ʼ��ɵó����ۣ�
�ڷ�������������õ��������ε����ʣ���ȫ�������ε��������PC��BC�����ɵó����ۣ�
��3�����жϳ���PMG=��AHP����SSS�жϳ���PMN�ա�PHN���ó���AHP=��PMN�����ɵó����ۣ�
��1����a2+4a+4+|2a+b|��0��
����a+2��2+|2a+b|��0��
��a����2��b��4��
�ʴ�Ϊ����2��4��
��2������ͼ 1���ɣ�1��֪��b��4��
��B��0��4����
��OB��4��
�� P ��ֱ�� AB ���Ҳ࣬���� x ���ϣ�
�ߡ�APB��45�㣬
��OP��OB��4��
��P��4��0����
�ʴ�Ϊ����4��0����
���ɣ�1��֪ a����2��b��4��
��A����2��0����B��0��4����
��OA��2��OB��4��
�ߡ�ABP ��ֱ�������Σ��ҡ�APB��45�㣬
��ֻ�С�ABP��90�����BAP��90�㣬
��ͼ 3��
��������ABP��90��ʱ���ߡ�APB����BAP��45�㣬
��AB��PB ��
���� P �� PC��OB �� C��
���BPC+��CBP��90�㣬
�ߡ�CBP+��ABO��90 �㣬
���ABO����BPC��
����AOB����BCP��
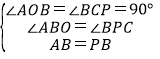
���AOB�ա�BCP��AAS����
��PC��OB��4��BC��OA��2��
��OC��OB��BC��2��
��P��4��2����
��������BAP��90��ʱ�� ���� P'�� P'D��OA �� D��
ͬ���ķ����ã���ADP'�ա�BOA��
��DP'��OA��2��AD��OB��4��
��OD��AD��OA��2��
��P'��2����2����
�������������ĵ� P��4��2����2����2����
��3����ͼ 2���ɣ�2��֪�� P��2����2����
��A����2��0����
��ֱ�� AP �Ľ���ʽΪ y����![]() x��1��
x��1��
��M��0����1����
��BM��5��
ͬ����ֱ�� BP �Ľ���ʽΪ y����3x+4��
��N��![]() ��0����
��0����
��MN��![]() ��
��
���� P �� PH��AB �� x ���� H��
�ߡ�BAP��90�㣬
���BAO+��PAH��90�㣬
���BAO+��ABM��90�㣬
���ABM����PAH��
����ABM����PAH��
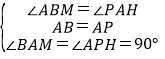 ��
��
���ABM�ա�PAH��ASA����
���AMB����PHA��AH��BM��5��
���PMG����PHA��OH��AH��OA��3��
��H��3��0����
��NH��3��![]() ��
��![]() ��MN��
��MN��
��P��2����2����M��0����1����H��3��0����
��PM��![]() ��PH��
��PH��![]() ��
��
��PM��PH��
���PNM�ա�PNH��SSS����
���AHP����PMN��
���PMG����PMN��
����MP ����BMN ��һ����ǵ�ƽ���ߣ�