题目内容
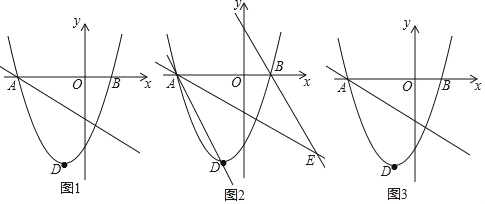
【题目】如图,已知抛物线![]() 与直线
与直线![]() 交于点O(0,0),
交于点O(0,0),![]() 。点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E。
。点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E。

(1)求抛物线的函数解析式;
(2)若点C为OA的中点,求BC的长;
(3)以BC,BE为边构造条形BCDE,设点D的坐标为(m,n),求m,n之间的关系式。
【答案】解:(1)∵点![]() 在直线
在直线![]() 上,∴
上,∴![]() ,即
,即![]() 。
。
∴点A的坐标是(6,12)。
又∵点A(6,12)在抛物线![]() 上,
上,
∴把A(6,12)代入![]() ,得
,得![]() 。
。
∴抛物线的函数解析式为![]() 。
。
(2)∵点C为OA的中点,∴点C的坐标是(3,6)。
把![]() 代入
代入![]() ,解得
,解得![]() (舍去)。
(舍去)。
∴![]() 。
。
(3)∵点D的坐标为(m,n),∴点E的坐标为![]() ,点C的坐标为
,点C的坐标为![]() 。
。
∴点B的坐标为![]() 。
。
把![]() 代入
代入![]() ,得
,得![]() ,即
,即![]() 。
。
∴m,n之间的关系式为![]() 。
。
【解析】
(1)根据点在曲线上,点的坐标满足于方程的关系,先求得由点A在直线![]() 上求得点A的坐标,再由点A在抛物线
上求得点A的坐标,再由点A在抛物线![]() 上,求得
上,求得![]() ,从而得到抛物线的函数解析式。
,从而得到抛物线的函数解析式。
(2)由于点B,C的纵坐标相等,从而由点C为OA的中点求得点C的坐标,将其纵坐标代入![]() ,求得
,求得![]() ,即可得到BC的长。
,即可得到BC的长。
(3)根据题意求出点B的坐标,代入![]() 即可求得m,n之间的关系式。
即可求得m,n之间的关系式。

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目