ЬтФПФкШн
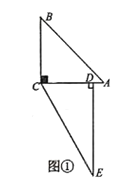
ЁОЬтФПЁПШчЭМ1ЃЌЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌЫФБпаЮADEFЪЧе§ЗНаЮЃЌDЁЂFЗжБ№дкABЁЂACБпЩЯЃЌДЫЪБBD=CFЃЌBDЁЭCFГЩСЂЃЎ
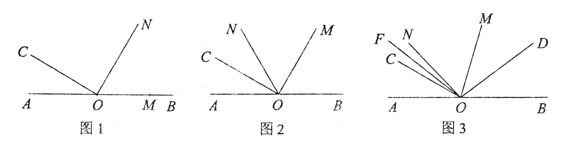
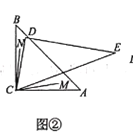
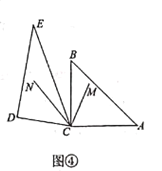
ЃЈ1ЃЉЕБе§ЗНаЮADEFШЦЕуAФцЪБеыа§зЊІШЃЈ0ЁуЃМІШЃМ90ЁуЃЉЪБЃЌШчЭМ2ЃЌBD=CFГЩСЂТ№ЃПШєГЩСЂЃЌЧыжЄУїЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЎ
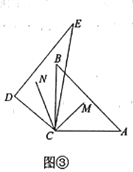
ЃЈ2ЃЉЕБе§ЗНаЮADEFШЦЕуAФцЪБеыа§зЊ45ЁуЪБЃЌШчЭМ3ЃЌбгГЄBDНЛCFгкЕуGЃЎ
ЂйЧѓжЄЃКBDЁЭCFЃЛ
ЂкЕБAB=4ЃЌAD=![]() ЪБЃЌЧѓЯпЖЮBGЕФГЄЃЎ
ЪБЃЌЧѓЯпЖЮBGЕФГЄЃЎ
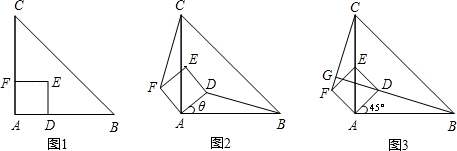
ЁОД№АИЁПНтЃКЃЈ1ЃЉBD=CFГЩСЂЁЃРэгЩШчЯТЃК
ЁпЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌЫФБпаЮADEFЪЧе§ЗНаЮЃЌ
ЁрAB=ACЃЌAD=AFЃЌЁЯBAC=ЁЯDAF=90ЁуЁЃ
ЁпЁЯBAD=ЁЯBACЉЁЯDACЃЌЁЯCAF=ЁЯDAFЉЁЯDACЃЌЁрЁЯBAD=ЁЯCAFЁЃ
дкЁїBADКЭЁїCAFжаЃЌЁпAB=ACЃЌЁЯBAD=ЁЯCAFЃЌ
ЁрЁїBADЁеЁїCAFЃЈSASЃЉЁЃЁрBD=CFЁЃ
ЃЈ2ЃЉЂйжЄУїЃКЩшBGНЛACгкЕуMЃЎ
ЁпЁїBADЁеЁїCAFЃЈвбжЄЃЉЃЌЁрЁЯABM=ЁЯGCMЁЃ
гжЁпЁЯBMA=ЁЯCMGЃЌЁрЁїBMAЁзЁїCMGЁЃ
ЁрЁЯBGC=ЁЯBAC=90ЁуЁЃЁрBDЁЭCFЁЃ
ЂкЙ§ЕуFзїFNЁЭACгкЕуNЁЃ
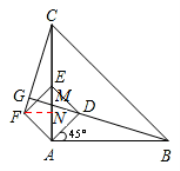
Ёпдке§ЗНаЮADEFжаЃЌAD=DE=![]() ЃЌ
ЃЌ
Ёр![]() ЁЃ
ЁЃ
ЁрAN=FN=![]() AE=1ЁЃ
AE=1ЁЃ
ЁпдкЕШбќжБНЧЁїABC жаЃЌAB=4ЃЌЁрCN=ACЉAN=3ЃЌ![]() ЁЃ
ЁЃ
ЁрдкRtЁїFCNжаЃЌ![]() ЁЃ
ЁЃ
дкRtЁїABMжаЃЌ![]() ЁЃ
ЁЃ
ЁрAM=![]() ЁЃ
ЁЃ
ЁрCM=ACЉAM=4Љ![]() ЃЌ
ЃЌ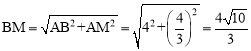 ЁЃ
ЁЃ
ЁпЁїBMAЁзЁїCMGЃЌЁр![]() ЃЌМД
ЃЌМД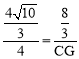 ЃЌЁрCG=
ЃЌЁрCG=![]() ЁЃ
ЁЃ
ЁрдкRtЁїBGCжаЃЌ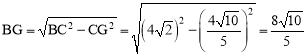 ЁЃ
ЁЃ
ЁОНтЮіЁПЃЈ1ЃЉЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌЫФБпаЮADEFЪЧе§ЗНаЮЃЌвзжЄЕУЁїBADЁеЁїCAFЃЌИљОнШЋЕШШ§НЧаЮЕФЖдгІБпЯрЕШЃЌМДПЩжЄЕУBD=CFЁЃ
ЃЈ2ЃЉЂйгЩЁїBADЁеЁїCAFЃЌПЩЕУЁЯABM=ЁЯGCMЃЌгжгЩЖдЖЅНЧЯрЕШЃЌвзжЄЕУЁїBMAЁзЁїCMGЃЌИљОнЯрЫЦШ§НЧаЮЕФЖдгІНЧЯрЕШЃЌПЩЕУBGC=ЁЯBAC=90ЁуЃЌМДПЩжЄЕУBDЁЭCFЁЃ
ЂкЪзЯШЙ§ЕуFзїFNЁЭACгкЕуNЃЌРћгУЙДЙЩЖЈРэМДПЩЧѓЕУAEЃЌBCЕФГЄЃЌМЬЖјЧѓЕУANЃЌCNЕФГЄЃЌгжгЩЕШНЧЕФШ§НЧКЏЪ§жЕЯрЕШЃЌПЩЧѓЕУAM=![]() ЁЃШЛКѓРћгУЁїBMAЁзЁїCMGЃЌЧѓЕУCGЕФГЄЃЌдйгЩЙДЙЩЖЈРэМДПЩЧѓЕУЯпЖЮBGЕФГЄЁЃ
ЁЃШЛКѓРћгУЁїBMAЁзЁїCMGЃЌЧѓЕУCGЕФГЄЃЌдйгЩЙДЙЩЖЈРэМДПЩЧѓЕУЯпЖЮBGЕФГЄЁЃ

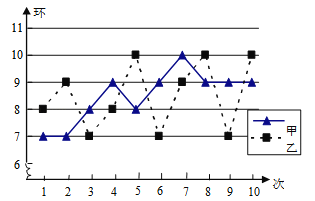
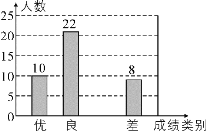
ЁОЬтФПЁПФГаЃАЫФъМЖСНИіАрЃЌИїбЁХЩ10УћбЇЩњВЮМгбЇаЃОйааЕФЁАНЈФЃЁБДѓШќдЄШќЃЌИїВЮШќбЁЪжЕФГЩМЈШчЯТЃК
АЫЃЈ1ЃЉАрЃК88ЃЌ91ЃЌ92ЃЌ93ЃЌ93ЃЌ93ЃЌ94ЃЌ98ЃЌ98ЃЌ100ЃЛ
АЫЃЈ2ЃЉАрЃК89ЃЌ93ЃЌ93ЃЌ93ЃЌ95ЃЌ96ЃЌ96ЃЌ98ЃЌ98ЃЌ99.
ЭЈЙ§ећРэЃЌЕУЕНЪ§ОнЗжЮіБэШчЯТЃК
АрМЖ | зюИпЗж | ЦНОљЗж | жаЮЛЪ§ | жкЪ§ | ЗНВю |
АЫЃЈ1ЃЉАр | 100 |
| 93 | 93 | 12 |
АЫЃЈ2ЃЉАр | 99 | 95 |
|
| 8.4 |
ЃЈ1ЃЉжБНгаДГіБэжа![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЕФжЕЮЊЃК
ЕФжЕЮЊЃК![]() _____ЃЌ
_____ЃЌ![]() _____ЃЌ
_____ЃЌ![]() _____ЃЛ
_____ЃЛ
ЃЈ2ЃЉвРОнЪ§ОнЗжЮіБэЃЌгаШЫЫЕЃКЁАзюИпЗждкЃЈ1ЃЉАрЃЌЃЈ1ЃЉАрЕФГЩМЈБШЃЈ2ЃЉАрКУ.ЁБЕЋвВгаШЫЫЕЃЈ2ЃЉАрЕФГЩМЈвЊКУ.ЧыИјГіСНЬѕжЇГжАЫЃЈ2ЃЉАрГЩМЈКУЕФРэгЩЃЛ
ЃЈ3ЃЉбЇаЃДгЦНОљЪ§ЁЂжаЮЛЪ§ЁЂжкЪ§ЁЂЗНВюжабЁШЁШЗЖЈСЫвЛИіГЩМЈЃЌЕШгкЛђДѓгкетИіГЩМЈЕФбЇЩњБЛЦРЖЈЮЊЁАгХауЁБЕШМЖЃЌШчЙћАЫЃЈ2ЃЉАргавЛАыЕФбЇЩњФмЙЛДяЕНЁАгХауЁБЕШМЖЃЌШЯЮЊетИіГЩМЈгІЖЈЮЊ_____Зж.