Question

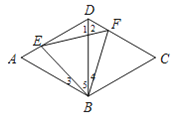
【题目】如图，在菱形ABCD中，点 E、F分别为边 AD、CD上的动点(都与菱形的顶点不重合)，联结 EF、BE、BF ．

（1）若∠A＝60°，且 AE+CF＝AB，判断△BEF 的形状，并说明理由；

（2）在（1）的条件下，设菱形的边长为a，求△BEF面积的最小值．

Answer 1

【答案】（1）△BEF的形状为等边三角形（2）

【解析】试题分析：（1）通过证明BE=BF，求出∠EBF的度数，可判断△BEF是等边三角形．

（2）当BE⊥AD时，BE最小，此时，S△BEF最小．求出此时的边EF长，及其对应高BM的长，按照三角形的面积公式即可求出．

试题解析：解：（1）△BEF的形状为等边三角形．证明如下：

如图，在菱形ABCD中，∠A=60°，∴AB∥DC，AB=BC=CD=DA，∴∠ADC=120°，∴∠1=∠2=60°，∴∠ABD=∠1=∠A=60°，∴AB=BD，∠A=∠2．

∵AE+CF=AB，DF+CF=CD，∴AE=DF，∴△ABE≌△DBF，∴BE=BF，∠3=∠4．

又∵∠3+∠5=60°，∴∠4+∠5=60°，∴△BEF为等边三角形．

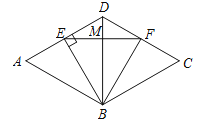
（2）如图，当BE⊥AD时，BE最小，此时，S△BEF最小．

设此时EF与BD交于点M，∴∠ABE=∠DBE=30°．

∵∠BEM=60°，∴∠BME=90°．

在Rt△ABE中，AB=a，∴．

在Rt△BEM中，∠BEM=60°，∴．

∴．