题目内容
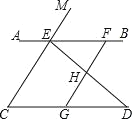
【题目】如图,已知点E,F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=70°,∠D=30°,求∠AEM的度数.
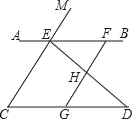
【答案】(1)证明见解析;(2)∠AED+∠D=180°;(3)∠AEM=100°.
【解析】
(1)根据同位角相等,两直线平行,可证CE∥GF;
(2)根据平行线的性质可得∠C=∠FGD,根据等量关系可得∠FGD=∠EFG,根据内错角相等,两直线平行可得AB∥CD,再根据平行线的性质可得∠AED与∠D之间的数量关系;
(3)根据对顶角相等可求∠DHG,根据三角形外角的性质可求∠CGF,根据平行线的性质可得∠C,∠AEC,再根据平角的定义可求∠AEM的度数.
(1)∵∠CED=∠GHD,
∴CE∥GF;
(2)∵CE∥GF,
∴∠C=∠FGD,
∵∠C=∠EFG,
∴∠FGD=∠EFG,
∴AB∥CD,
∴∠AED+∠D=180°;
(3)∵∠DHG=∠EHF=70°,∠D=30°,
∴∠CGF=70°+30°=100°,
∵CE∥GF,
∴∠C=180°﹣100°=80°,
∵AB∥CD,
∴∠AEC=80°,
∴∠AEM=180°﹣80°=100°.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目