题目内容
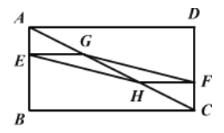
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 分别是边
分别是边![]() 上的动点(点
上的动点(点![]() 不与
不与![]() 重合),且
重合),且![]() ,过点
,过点![]() 作
作![]() 的平行线
的平行线![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,设
,设![]() 为
为![]() .
.
(1)试说明不论![]() 为何值时,总有
为何值时,总有![]() ∽
∽![]() ;
;
(2)是否存在一点![]() ,使得四边形
,使得四边形![]() 为平行四边形,试说明理由;
为平行四边形,试说明理由;
(3)当![]() 为何值时,四边形
为何值时,四边形![]() 的面积最大,并求出最大值.
的面积最大,并求出最大值.

【答案】(1)见解析;(2)当![]() 时,四边形
时,四边形![]() 为平行四边形;(3)当
为平行四边形;(3)当![]() 时,四边形
时,四边形![]() 的面积最大,最大值为
的面积最大,最大值为![]() .
.
【解析】
(1)根据题意得到∠MQB=∠CAB,根据相似三角形的判定定理证明;
(2)根据对边平行且相等的四边形是平行四边形解答;
(3)根据勾股定理求出BC,根据相似三角形的性质用x表示出QM、BM,根据梯形面积公式列出二次函数解析式,根据二次函数性质计算即可.
解:(1)∵![]() ,
,
∴![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ∽
∽![]() ;
;
(2)当![]() 时,四边形
时,四边形![]() 为平行四边形,
为平行四边形,
∵![]() ,
,![]() ,
,
∴四边形![]() 为平行四边形;
为平行四边形;
(3)∵![]() ,
,
∴![]() ,
,
∵![]() ∽
∽![]() ,
,
∴![]() ,即
,即![]() ,
,
解得,![]() ,
,
∵![]() ,
,
∴![]() ,即
,即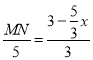 ,
,
解得,![]() ,
,
则四边形![]() 的面积
的面积![]() ,
,
∴当![]() 时,四边形
时,四边形![]() 的面积最大,最大值为
的面积最大,最大值为![]() .
.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
【题目】甲、乙两个工程队需完成A、B两个工地的工程.若甲、乙两个工程队分别可提供40个和50个标准工作量,完成A、B两个工地的工程分别需要70个和20个标准工作量,且两个工程队在A、B两个工地的1个标准工作量的成本如下表所示:
A工地 | B工地 | |
甲工程队 | 800元 | 750元 |
乙工程队 | 600元 | 570元 |
设甲工程队在A工地投入x(20≤x≤40)个标准工作量,完成这两个工程共需成本y元.
(1)求y与x之间的函数关系式;
(2)请判断y是否能等于62000,并说明理由.