题目内容
【题目】如图,在矩形ABCD中,AB=3,BC=6,若点E,F分别在AB,CD上,且BE=2AE,DF=2FC,G,H分别是AC的三等分点,则四边形EHFG的面积为( )
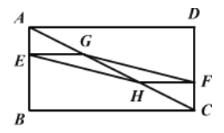
A. 1B. ![]() C. 2D. 4
C. 2D. 4
【答案】C
【解析】
如图,延长FH交AB于点M,由BE=2AE,DF=2FC,G、H分别是AC的三等分点,证明EG//BC,FH//AD,进而证明△AEG∽△ABC,△CFH∽△CAD,进而证明四边形EHFG为平行四边形,再根据平行四边形的面积公式求解即可.
如图,延长FH交AB于点M,
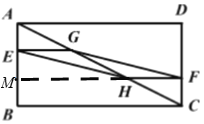
∵BE=2AE,DF=2FC,AB=AE+BE,CD=CF+DF,
∴AE:AB=1:3,CF:CD=1:3,
又∵G、H分别是AC的三等分点,
∴AG:AC=CH:AC=1:3,
∴AE:AB=AG:AC,CF:CD=CH:CA,
∴EG//BC,FH//AD,
∴△AEG∽△ABC,△CFH∽△CDA,BM:AB=CF:CD=1:3,∠EMH=∠B,
∴EG:BC=AE:AB=1:3,HF:AD=CF:CD=1:3,
∵四边形ABCD是矩形,AB=3,BC=6,
∴CD=AB=3,AD=BC=6,∠B=90°,
∴AE=1,EG=2,CF=1,HF=2,BM=1,
∴EM=3-1-1=1,EG=FH,
∴EG![]() FH,
FH,
∴四边形EHFG为平行四边形,
∴S四边形EHFG=2×1=2,
故选C.

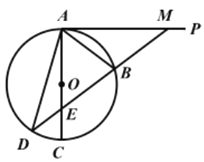
【题目】如图,AC是⊙O的一条弦,AP是⊙O的切线。作BM=AB并与AP交于点M,延长MB交AC于点E,交⊙O于点D,连接AD.
(1)求证:AB=BE;
(2)若⊙O的半径R=5,AB=6,求AD的长.
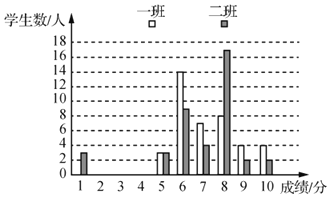
【题目】8年级某老师对一、二班学生阅读水平进行测试,并将成绩进行了统计,绘制了如下图表(得分为整数,满分为10分,成绩大于或等于6分为合格,成绩大于或等于9分为优秀).
平均分 | 方差 | 中位数 | 众数 | 合格率 | 优秀率 | |
一班 | 7.2 | 2.11 | 7 | 6 | 92.5% | 20% |
二班 | 6.85 | 4.28 | 8 | 8 | 85% | 10% |
根据图表信息,回答问题:
(1)用方差推断, 班的成绩波动较大;用优秀率和合格率推断, 班的阅读水平更好些;
(2)甲同学用平均分推断,一班阅读水平更好些;乙同学用中位数或众数推断,二班阅读水平更好些.你认为谁的推断比较科学合理,更客观些.为什么?