题目内容
【题目】在![]() 中,
中,![]() 于点
于点![]() ,点
,点![]() 是射线
是射线![]() 上一点,连接
上一点,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,且交直线
,且交直线![]() 于点
于点![]() .
.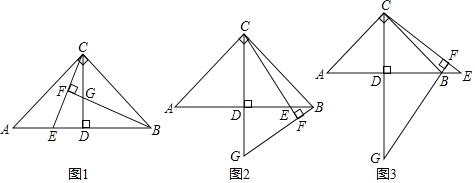
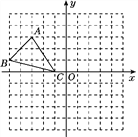
(1)如图1,当点![]() 在线段
在线段![]() 上时,求证:
上时,求证:![]() .
.
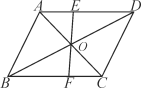
(2)如图2,当点![]() 在线段
在线段![]() 上时,其它条件不变,请猜想
上时,其它条件不变,请猜想![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
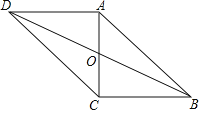
(3)如图3,当点![]() 在线段
在线段![]() 的延长线上时,其它条件不变,请直接写出
的延长线上时,其它条件不变,请直接写出![]() 与
与![]() 之间的数量关系.
之间的数量关系.
【答案】(1)见解析;(2)AE=CG,理由见解析;(3)CG=AE
【解析】
(1)根据等腰直角三角形的性质得到∠A=∠ABC,根据同角的余角相等得到∠CBG=∠ACE,根据ASA证明△ACE≌△CBG,即可得出结论;
(2)同理即可证明△ACE≌△CBG,即可得出结论;
(3)同(2)可得∠A=∠GCB=45°,证得∠CGB=∠AEC,可证明△ACE≌△CBG,即可得出结论.
(1)∵在△ABC中,AC=BC,∠ACB=90°,
∴∠A=∠ABC=45°.
∵点D是AB的中点,
∴∠BCG=![]() ∠ACB=45°,
∠ACB=45°,
∴∠A=∠BCG.
∵BF⊥CE,
∴∠CBG+∠BCF=90°.
∵∠ACE+∠BCF=90°,
∴∠CBG=∠ACE,
在△ACE和△CBG中,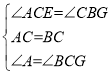 ,
,
∴△ACE≌△CBG(ASA),
∴AE=CG;
(2)AE=CG;理由如下:
∵在△ABC中,AC=BC,∠ACB=90°,
∴∠A=∠ABC=45°.
∵点D是AB的中点,
∴∠BCG=![]() ∠ACB=45°,
∠ACB=45°,
∴∠A=∠BCG.
∵BF⊥CE,
∴∠CBG+∠BCF=90°.
∵∠ACE+∠BCF=90°,
∴∠CBG=∠ACE,
在△ACE和△CBG中,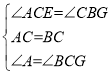 ,
,
∴△ACE≌△CBG(ASA),
∴AE=CG;
(3)CG=AE.
证明:同(1)(2)可得∠A=∠GCB=45°,
∵BF⊥CE,
∴∠GDB=∠BFE=90°,
∵∠DBG=∠FBE,
∴∠CGB=∠AEC,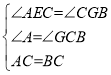 ,
,
∴△ACE≌△CBG(AAS),
∴CG=AE.