题目内容
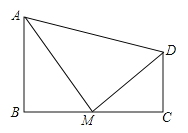
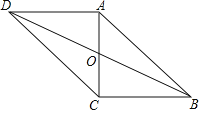
【题目】如图,在ABCD中,对角线AC、BD交于点O,AC⊥BC,且ABCD的周长为36,△OCD的周长比△OBC的周长大2.
(1)求BC,CD的长;
(2)求ABCD的面积.
【答案】(1)BC=8,CD=10;(2)48.
【解析】
(1)因为AD=BC,AB=CD,OA=OC,求出DC+BC=18,DC-BC=2,解方程组即可得出答案.
(2)利用勾股定理可求出AC的长,进而可求出ABCD的面积.
(1)∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,AO=OC,
∵平行四边形ABCD的周长为18,
∴DC+BC=18①,
∵△OCD的周长比△OBC的周长大2,
∴(CD+OD+OC)-(BC+OB+OC)=2,
∴CD-BC=2②,
①+②得:2CD=20,
CD=10,
①-②得:2BC=16,
BC=8;
(2)∵BC=8,AB=CD=10,AC⊥BC,
∴AC=![]() =6,
=6,
∴ABCD的面积=6×8=48.

练习册系列答案
相关题目