Question

【题目】如图，在平面直角坐标系中，四边形OABC是正方形，过点B（2，2）的直线l与y轴交于点D，且OD=AD，直线l上的点E在第三象限，且到x轴的距离为 ．
（1）求直线l的表达式；
（2）若反比例函数y= 的图象经过点E，求k的值．

Answer 1

【答案】
（1）解：∵B（2，2），四边形OABC是正方形，

∴OA=2，

∵OD=AD，

∴OD=1，

∴D（0，1），

设直线l的表达式为y=kx+b，则

，

解得： ，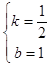

∴直线l的表达式为：y= x+1

（2）解：∵点E到x轴的距离为 ，且点E在第三象限，

∴点E的纵坐标为﹣ ，

又∵点E在直线l上，

∴ x+1=﹣ ，

∴x=﹣3，

∴点E的坐标是（﹣3，﹣ ），

∵反比例函数y= 的图象经过点E，

∴﹣ = ，

∴k=

【解析】（1）四边形OABC是正方形，过点B（2，2），求出A点的坐标，再根据OD=AD，求出D点的坐标，设直线l的表达式y=kx+b，把D点和B点的坐标代入，求出k，b的值，即可得出答案；（2）根据已知条件求出E点的纵坐标，再根据点E在直线l上，求出点E的坐标，最后根据反比例函数y= 的图象经过点E，把E点的坐标代入，求出k的值即可．