��Ŀ����
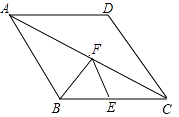
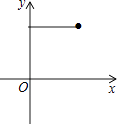
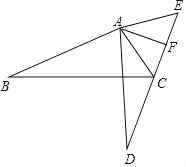
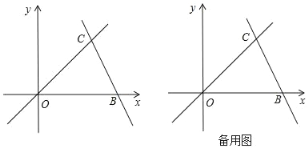
����Ŀ����ͼ��ֱ��OC��BC�ĺ�����ϵʽ�ֱ�Ϊy��x��y����2x+b���ҽ���C�ĺ�����Ϊ2������P��x��0�����߶�OB���ƶ���0��x��3����
��1�����C�������b��
��2������A��0��1������xΪ��ֵʱ��AP+CP��ֵ��С��
��3������P��ֱ��EF��x�ᣬ�ֱ�ֱ��OC��BC�ڵ�E��F��
����EF��3�����P�����꣮
�����OBC��λ��ֱ��EF��ಿ�ֵ����Ϊs����д��s��x֮��ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
���𰸡���1��b��6����2����![]() ��0������3����P��1��0������s��
��0������3����P��1��0������s��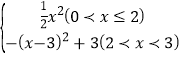 ��
��
��������
��1������C�ĺ��������ֱ��y=x�У������C���꣬��������C�������ֱ��BC����ʽ�У��������b��
��2�������öԳ���ȷ������C'�����꣬����AC'�ó���P��λ�ã����ô���ϵ�������ֱ��AC'�Ľ���ʽ���ɵó����ۣ�
��3���������ֱ��BC����ʽ�������ó���E��F�����꣬�����ó�EF�������EF=3����������⼴�ɵó����ۣ�
�ڷ�������������������ε������ʽ������IJ�ɵó����ۣ�
��1���ߵ�C��ֱ��OC��y��x�ϣ��ҵ�C�ĺ�����Ϊ2
���C��2��2����
�ߵ�C��ֱ��BC��y����2x+b�ϣ�
����2��2+b��2��
��b��6��
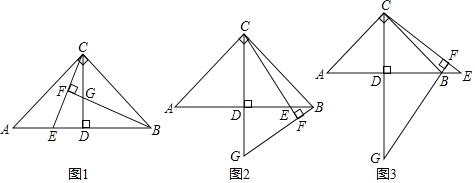
��2����ͼ1������C����x��ĶԳƵ�C��������AC'��x���ڵ�P����ʱAP+CP��AP+PC'��AC'��С��
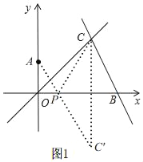
��C��2��2������C'��2����2����
�ߵ�A��0��1����
��ֱ��AC'�Ľ���ʽΪy����![]() x+1��
x+1��
��y��0��
��0����![]() x+1��
x+1��
��x��![]() ��
��
���P��������![]() ��0����
��0����
��3�����ɣ�1��֪��b��6��
��ֱ��BC�Ľ���ʽΪy����2x+6��
��EF��x����P��
��F��x����2x+6����
�ߵ�E��ֱ��OC�ϣ�
��E��x��x����
��EF��|��2x+6��x|��|3x��6|��
��EF��3��
��|3x��6|��3��
��x��3���ᣩ��x��1��
��P��1��0����
�ڵ�0��x��2ʱ����ͼ2��
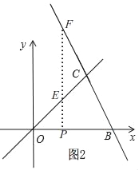
��E��x��x����
��OP��x��PE��x��
��s��S��OPE��![]() OP��PE��
OP��PE��![]() x2��
x2��
��2��x��3ʱ����ͼ3��
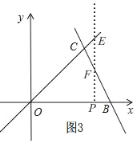
�ɣ�2��֪��ֱ��BC�Ľ���ʽΪy����2x+6��
��B��3��0����
��P��x��0����
��F��x����2x+6����
��BP��3��x��PF����2x+6��
��s��S��OBC��S��BPF��![]() ��3��2��
��3��2��![]() ��3��x������2x+6��������x��3��2+3��
��3��x������2x+6��������x��3��2+3��
����s��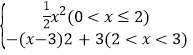 .
.

 ����������ϵ�д�
����������ϵ�д�