Question

【题目】如图，是等边三角形内一点，将线段绕点顺时针旋转60°得到线段，连接．若，，，则四边形的面积为___________．

Answer 1

【答案】6+4

【解析】

连结PP′，如图，由等边三角形的性质得到∠BAC=60°，AB=AC，由旋转的性质得到CP=CP′=4，∠PCP′=60°，得到△PCP′为等边三角形，求得PP′=PC=4，根据全等三角形的性质得到AP′=PB=5，根据勾股定理的逆定理得到△APP′为直角三角形，∠APP′=90°，根据三角形的面积公式即可得到结论．

连结PP′，如图，

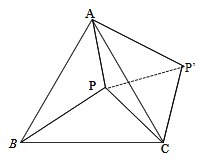
∵△ABC为等边三角形，
∴∠BAC=60°，AB=AC，
∵线段CP绕点C顺时针旋转60°得到线段CP'，
∴CP=CP′=4，∠PCP′=60°，
∴△PCP′为等边三角形，
∴PP′=PC=4，
∵∠ACP+∠BCP=60°，∠ACP+∠ACP′=60°，
∴∠BCP=∠ACP′，且AC=BC，CP=CP′
∴△BCP≌△ACP′（SAS），
∴AP′=PB=5，
在△APP′中，∵PP′2=42=16，AP2=32=9，AP′2=52=25，
∴PP′2+AP2=AP′2，
∴△APP′为直角三角形，∠APP′=90°，
∴S四边形APCP′=S△APP′+S△PCP′= AP×PP′+ ×PP′2=6+4 ，
故答案为：6+4．