题目内容
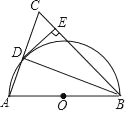
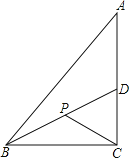
【题目】如图,正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上一个动点,连结
上一个动点,连结![]() ,过
,过![]() 作
作![]() ,
,![]() ,
,
![]() ,
,![]() 分别为垂足.
分别为垂足.
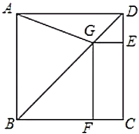
(1)求证:![]() ;
;
(2)①写出![]() 、
、![]() 、
、![]() 三条线段满足的等量关系,并证明;②求当
三条线段满足的等量关系,并证明;②求当![]() ,
,![]() 时,
时,![]() 的长
的长
【答案】(1)见解析;(2)①GE2+GF2=AG2,证明见解析;②![]() 的长为
的长为![]() 或
或![]() .
.
【解析】
(1)根据正方形的性质得出△DGE和△BGF是等腰直角三角形,可得GE=![]() DG,GF=
DG,GF=![]() BG,结合AB=
BG,结合AB=![]() BD即可得出结论;
BD即可得出结论;
(2)①连接CG,由SAS证明△ABG≌△CBG,得出AG=CG,证出四边形EGFC是矩形,得出CE=GF,由勾股定理即可得出GE2+GF2=AG2;
②设GE=CF=x,则GF=BF=6x,由①中结论得出方程求出CF=1或CF=5,再分情况讨论,由勾股定理求出BG即可.
解:(1)∵四边形ABCD为正方形,
∴∠BCD=90°,∠ABD=∠CDB=∠CBD=45°,AB=BC=CD,
∴△ABD是等腰直角三角形,
∴AB=![]() BD,
BD,
∵GE⊥CD,GF⊥BC,
∴△DGE和△BGF是等腰直角三角形,
∴GE=![]() DG,GF=
DG,GF=![]() BG,
BG,
∴GE+GF=![]() (DG+BG)=
(DG+BG)=![]() BD,
BD,
∴GE+GF=AB;
(2)①GE2+GF2=AG2,
证明:连接CG,如图所示:
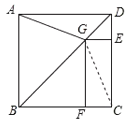
在△ABG和△CBG中,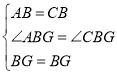 ,
,
∴△ABG≌△CBG(SAS),
∴AG=CG,
∵GE⊥CD,GF⊥BC,∠BCD=90°,
∴四边形EGFC是矩形,
∴CE=GF,
∵GE2+CE2=CG2,
∴GE2+GF2=AG2;
②设GE=CF=x,则GF=BF=6x,
∵GE2+GF2=AG2,
∴![]() ,
,
解得:x=1或x=5,
当x=1时,则BFGF=5,
∴BG=![]() ,
,
当x=5时,则BF=GF=1,
∴BG=![]() ,
,
综上,![]() 的长为
的长为![]() 或
或![]() .
.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目