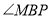题目内容
【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下列四个结论:

①AD和EF互相垂直平分;
②AE=AF;
③当∠BAC=90°时,AD=EF;
④DE是AB的垂直平分线.
其中正确的是_________________(填序号).
【答案】②③
【解析】
根据角平分线的性质得到DE=DF,证明Rt△AED≌Rt△AFD,根据全等三角形的性质、线段垂直平分线的判定定理以及矩形的判定与性质进行逐一判断.
解:∵AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,∴DE=DF,
在△AED和△AFD中,![]() ,∴Rt△AED≌Rt△AFD(HL),∴AE=AF,又DE=DF,∴AD垂直平分EF,而EF不一定垂直平分AD,故①错误,②正确;
,∴Rt△AED≌Rt△AFD(HL),∴AE=AF,又DE=DF,∴AD垂直平分EF,而EF不一定垂直平分AD,故①错误,②正确;
∵∠BAC=90°,∴∠EAF=∠AED=∠AFD=90°,∴四边形AEDF为矩形,∴AD=EF,故③正确;
∵DE⊥AB,而AD与BD不一定相等,∴不能得出DE是AB的垂直平分线,④错误;
故答案为:②③.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目