题目内容
在⊙O中,弦AB所对的圆周角之间的关系为______.
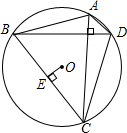
如图:
①若点D与C在优弧
上,
则∠ACB=∠ADB;
②若C在优弧
上,E在劣弧
上,
则四边形AEBC是⊙O的内接四边形,
可得:∠ACB+∠AEB=180°;
故在⊙O中,弦AB所对的圆周角之间的关系为:相等或互补.
故答案为:相等或互补.

①若点D与C在优弧
 |
| ACB |
则∠ACB=∠ADB;
②若C在优弧
 |
| ACB |
 |
| AB |
则四边形AEBC是⊙O的内接四边形,
可得:∠ACB+∠AEB=180°;
故在⊙O中,弦AB所对的圆周角之间的关系为:相等或互补.
故答案为:相等或互补.


练习册系列答案
相关题目