题目内容
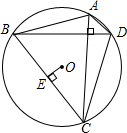
如图所示，四边形ABCD的四个顶点在⊙O上，AC，BD是对角线，且AC⊥BD，OE⊥BC于E，探索：OE与AD的数量关系．
答：OE=
AD．
证明：连CO延长交⊙O于P，连接BP．
则∠CBP=90°；
∵OE⊥BC，由垂径定理，得BE=EC；
又∵BE=EC，PO=OC，
∴OE是△PBC的中位线，
∴OE=
BP；
∵∠1=∠2，∠PBD=90°-∠1，∠ADB=90°-∠2，
∴∠PBD=∠ADB，
=
；
∴
=
；
故BP=AD，即OE=
BP=
AD．
| 1 |
| 2 |
证明：连CO延长交⊙O于P，连接BP．
则∠CBP=90°；
∵OE⊥BC，由垂径定理，得BE=EC；
又∵BE=EC，PO=OC，
∴OE是△PBC的中位线，
∴OE=
| 1 |
| 2 |
∵∠1=∠2，∠PBD=90°-∠1，∠ADB=90°-∠2，
∴∠PBD=∠ADB，
 |
| PD |
|
| AB |
∴
|
| PB |
|
| AD |
故BP=AD，即OE=
| 1 |
| 2 |
| 1 |
| 2 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
