题目内容
【题目】如图,四边形ABCD是菱形,点G是BC延长线上一点,连结AG,分别交BD、CD于点E、F,连结CE.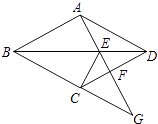
(1)求证:∠DAE=∠DCE;
(2)当CE=2EF时,EG与EF的等量关系是 .
【答案】
(1)
证明:∵四边形ABCD是菱形,
∴AD=CD,∠ADE=∠CDB;
在△ADE和△CDE中,
 .
.
∴△ADE≌△CDE,
∴∠DAE=∠DCE.
(2)FG=3EF
【解析】(2.)解:理由:∵四边形ABCD是菱形,
∴AD∥BC,
∴∠DAE=∠G,
由题意知:△ADE≌△CDE
∴∠DAE=∠DCE,
则∠DCE=∠G,
∵∠CEF=∠GEC,
∴△ECF∽△EGC,
∴ ![]() =
= ![]() ,
,
∵EC=2EF,
∴ ![]() =
= ![]() ,
,
∴EG=2EC=4EF,
∴FG=EG﹣EF=4EF﹣EF=3EF.
故答案为FG=3EF.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目