题目内容
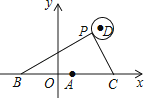
【题目】如图,反比例函数y= ![]() (x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.,则下列结论正确的是(将正确的结论填在横线上).
(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.,则下列结论正确的是(将正确的结论填在横线上).
①s△OEB=s△ODB , ②BD=4AD,③连接MD,S△ODM=2S△OCE , ④连接ED,则△BED∽△BCA.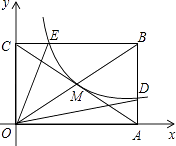
【答案】①④
【解析】解:∵四边形ABCD是矩形,
∴S△OBC=S△OBA ,
∵点E、点D在反比例函数y= ![]() (x>0)的图象上,
(x>0)的图象上,
∴S△CEO=S△OAD= ![]() ,
,
∴S△OEB=S△OBD , 故①正确,
设点B(m,n),D(m,n′)则M( ![]() m,
m, ![]() n,),
n,),
∵点M,点D在反比例函数y= ![]() (x>0)的图象上,
(x>0)的图象上,
∴ ![]() m
m ![]() n=mn′,
n=mn′,
∴n′= ![]() n,
n,
∴AD= ![]() AB,
AB,
∴BD=3AD,故②错误,
连接DM,∵S△ODM=S△OBD﹣S△BDM= ![]()
![]() ba﹣
ba﹣ ![]()
![]() b
b ![]() a=
a= ![]() ab,
ab,
∵S△CEO=S△OAD= ![]() a
a ![]() b=
b= ![]() ab,
ab,
∴S△ODM:S△OCE= ![]() ab:
ab: ![]() ab=3:2,故③错误,
ab=3:2,故③错误,
连接DE,同法可证CE= ![]() BC,
BC,
∴BE=3EC,
∴ ![]() =
= ![]() =3,
=3,
∴DE∥AC,
∴△BED∽△BCA,故④正确.
所以答案是①④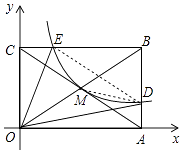
【考点精析】关于本题考查的反比例函数的图象和反比例函数的性质,需要了解反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点;性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大才能得出正确答案

 通城学典默写能手系列答案
通城学典默写能手系列答案【题目】某校积极参与垃圾分类活动,以班级为单位收集可回收的垃圾,下面是七年级各班一周收集的可回收垃圾的质量频数表和频数直方图(每组含前一个边界值,不含后一个边界值).
某校七年级各班一周收集的可回收垃圾的质量频数表
组别(kg) | 频数 |
4.0~4.5 | 2 |
4.5~5.0 | a |
5.0~5.5 | 3 |
5.5~6.0 | 1 |
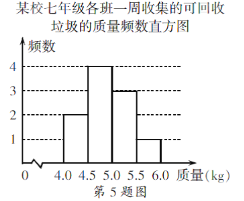
(1)求a的值;
(2)已知收集的可回收垃圾以0.8元/kg被回收,该年级这周收集的可回收垃圾被回收后所得的金额能否达到50元.