题目内容
【题目】如图,在等腰直角三角形ABC中,∠BAC=90°,AC=8 ![]() cm,AD⊥BC于点D.点P从点A出发,沿A→C方向以
cm,AD⊥BC于点D.点P从点A出发,沿A→C方向以 ![]() cm/s的速度运动到点C停止.在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2)
cm/s的速度运动到点C停止.在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2)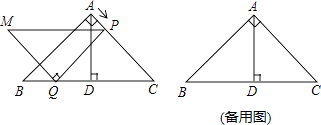
(1)当点M落在AB上时,求x的值;
(2)当点M落在AD上时,PM与CD之间的数量关系是 , 此时x的值是;
(3)求y关于x的函数解析式,并写出自变量x的取值范围.
【答案】
(1)
解:当点M落在AB上时,四边形AMQP是正方形,此时点D与点Q重合,
∴AP=CP=4 ![]() ,所以x=
,所以x= ![]() =4.
=4.
故答案为4.
(2)PM= ![]() CD;
CD;![]()
(3)
解:①当0<x≤4时,如图2中,设PM、PQ分别交AD于点E、F,则重叠部分为△PEF,
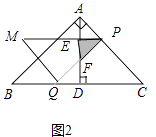
∵AP= ![]() x,
x,
∴EF=PE=x,
∴y=S△PEF= ![]() PEEF=
PEEF= ![]() x2.
x2.
②当4<x≤ ![]() 时,如图3中,设PM、MQ分别交AD于E、G,则重叠部分为四边形PEGQ.
时,如图3中,设PM、MQ分别交AD于E、G,则重叠部分为四边形PEGQ.
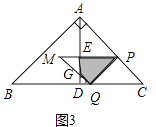
∵PQ=PC=8 ![]() ﹣
﹣ ![]() x,
x,
∴PM=16﹣2x,∴ME=PM﹣PE=16﹣3x,
∴y=S△PMQ﹣S△MEG= ![]() (8
(8 ![]() ﹣
﹣ ![]() x)2﹣
x)2﹣ ![]() (16﹣3x)2=﹣
(16﹣3x)2=﹣ ![]() x2+32x﹣64.
x2+32x﹣64.
③当 ![]() <x<8时,如图4中,则重合部分为△PMQ,
<x<8时,如图4中,则重合部分为△PMQ,
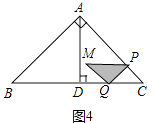
∴y=S△PMQ= ![]() PQ2=
PQ2= ![]() (8
(8 ![]() ﹣
﹣ ![]() x)2=x2﹣16x+64.
x)2=x2﹣16x+64.
综上所述y= 
【解析(1)当点M落在AB上时,四边形AMQP是正方形,此时点D与点Q重合,由此即可解决问题.(2)如图1中,当点M落在AD上时,作PE⊥QC于E,先证明DQ=QE=EC,由PE∥AD,得 ![]() ,由此即可解决问题.(3)分三种情形①当0<x≤4时,如图2中,设PM、PQ分别交AD于点E、F,则重叠部分为△PEF,②当4<x≤
,由此即可解决问题.(3)分三种情形①当0<x≤4时,如图2中,设PM、PQ分别交AD于点E、F,则重叠部分为△PEF,②当4<x≤ ![]() 时,如图3中,设PM、MQ分别交AD于E、G,则重叠部分为四边形PEGQ.③当
时,如图3中,设PM、MQ分别交AD于E、G,则重叠部分为四边形PEGQ.③当 ![]() <x<8时,如图4中,则重合部分为△PMQ,分别计算即可解决问题.
<x<8时,如图4中,则重合部分为△PMQ,分别计算即可解决问题.
【考点精析】本题主要考查了相似三角形的应用的相关知识点,需要掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能正确解答此题.