题目内容
【题目】已知关于
的方程组
，以下结论：
①
时，方程组的解也是方程
的解；
②论
取什么实数，
的值始终不变；
③若
，则
的最小值为
；
请判断以上结论是否正确，并说明理由．
【答案】结论①和结论②正确，结论③不正确，理由见解析
【解析】
先利用消元法求得方程组的解；
①将
代入方程组的解求得x，y的值，再代入方程中即可做出判断；
②将方程组的解代入
，化简即可做出判断；
③将方程组的解代入
，整理代数式求得最小值，即可做出判断．
解：结论①和结论②正确，结论③不正确，理由如下：
，
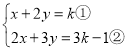由①×2②得：
，
将代入①得：
，
解得：
，
∴原方程组的解为
；
①当时，则原方程组的解为
，代入
得：
左边
=右边，
∴方程组的解也是方程的解，故①正确；
②∵
，
∴②论
取什么实数，的值始终不变，故②正确；
③∵
，
∵
，
∴
，即
的最小值为
，故③不正确；
∴结论①和结论②正确，结论③不正确．
练习册系列答案
阅读快车系列答案
相关题目
