题目内容
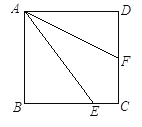
【题目】如图,正方形ABCD中,E为BC上一点,AF平分∠DAE,求证:BE+DF=AE.
【答案】证明见解析
【解析】
延长CB到G,使GB=DF,连接AG,易证△ADF≌△ABG,得到∠1=∠G,∠3=∠2=∠4,而∠1=∠4+∠5,则∠1=∠4+∠5=∠3+∠5=∠GAE,得到∠G=∠GAE,于是AE=GE=GB+BE=DF+BE,即可得到结论.
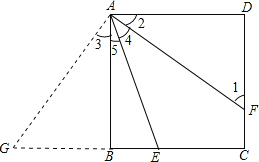
证明:延长CB到G,使GB=DF,连接AG(如图),
∵四边形ABCD为正方形,
∴AD=AB,∠B=∠D=90°
∴∠ABG=∠D=90°
∴△ADF≌△ABG,
∴∠1=∠G,∠3=∠2,DF=BG
∵AF平分∠DAE
∴∠2=∠4=∠3
又∵AB∥CD
∴∠1=∠4+∠5=∠3+∠5=∠GAE
∴∠G=∠GAE
∴AE=GE=GB+BE=DF+BE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目