题目内容
14.己知AD∥CE,点B为直线AD、CE所确定的平面内一点.(1)如图1所示,求证:∠ADB=∠B+∠BFE.
(2)如图2,FG平分∠BFE,DG交FG于点G交BF于点H,且∠BDG:∠ADG=2:1,∠B=20°,∠DGF=30°,求∠BHD的度数.

分析 (1)先延长BD交EF于N,根据平行线的性质以及∠BNE是△BFN的外角,可求得∠ADB=∠B+∠BFE;
(2)延长BD交FE于M,设∠BDG=α,根据AD∥FE,得出∠ADB=∠EMB=$\frac{3}{2}$α,再根据三角形内角和定理以及角平分线的定义,求得∠BFE=2α-20°,最后根据∠BFE是△BMF的外角,可得∠BFE=∠B+∠BME,得到2α-20°=20°+$\frac{3}{2}$α,求得∠BDH=80°,即可得到∠BHD=180°-20°-80°=80°.
解答 解:(1)如图1,延长BD交EF于N,
∵AD∥CE,
∴∠ADB=∠ENB,
∵∠BNE是△BFN的外角,
∴∠BNE=∠B+∠BFE,
∴∠ADB=∠B+∠BFE;
(2)如图2,延长BD交FE于M,设∠BDG=α,
∵∠BDG:∠ADG=2:1,
∴∠ADB=α+$\frac{1}{2}$α=$\frac{3}{2}$α,
∵AD∥FE,
∴∠ADB=∠EMB=$\frac{3}{2}$α,
∵DG交BF于点H,∠B=20°,∠DGF=30°,
∴∠BFG=α-10°,
∵FG平分∠BFE,
∴∠BFE=2α-20°,
∵∠BFE是△BMF的外角,
∴∠BFE=∠B+∠BME,
即2α-20°=20°+$\frac{3}{2}$α,
解得α=80°,
∴∠BDH=80°,
∴△BDH中,∠BHD=180°-20°-80°=80°.
点评 本题主要考查了平行线的性质、三角形内角和定理以及三角形外角性质的综合应用,解决问题的关键是作辅助线构造三角形,运用三角形的一个外角等于和它不相邻的两个内角的和进行计算.

练习册系列答案
相关题目
5.下列方程中是关于x的一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | 3x2+xy-y2=0 | C. | x2+x+1=0 | D. | x2+$\frac{1}{{x}^{2}}$=5 |
19. 如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点A的对应点A′的坐标是( )
如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点A的对应点A′的坐标是( )
 如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点A的对应点A′的坐标是( )
如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点A的对应点A′的坐标是( )| A. | (-1,2) | B. | (-9,18) | C. | (-9,18)或(9,-18) | D. | (-1,2)或(1,-2) |
6.下列事件中是随机事件的是( )
| A. | 三角形内角和180° | B. | 抛物线与x轴有2个交点 | ||
| C. | 若x2=4,则x=±2 | D. | 直径所对圆周角是100° |
10.有10个数,它们的平均数是45,将其中最小的4和最大的70这两个数去掉,则余下数的平均数为( )
| A. | 45 | B. | 46 | C. | 47 | D. | 48 |
 在长为am,宽为bm的一块草坪上修两条互相垂直且宽度都是1m的笔直小路,则余下草坪的面积可表示为(ab-a-b+1)m2.
在长为am,宽为bm的一块草坪上修两条互相垂直且宽度都是1m的笔直小路,则余下草坪的面积可表示为(ab-a-b+1)m2.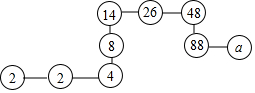 根据如图所示的规律.a的值为162.
根据如图所示的规律.a的值为162.