题目内容
【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°,若坡角∠FAE=30°,求大树的高度(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11, ![]() ≈1.73)
≈1.73)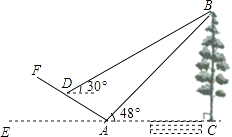
【答案】解:如图,过点D作DG⊥BC于G,DH⊥CE于H, 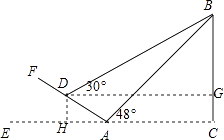
则四边形DHCG为矩形.
故DG=CH,CG=DH,DG∥HC,
∴∠DAH=∠FAE=30°,
在直角三角形AHD中,
∵∠DAH=30°,AD=6,
∴DH=3,AH=3 ![]() ,
,
∴CG=3,
设BC为x,
在直角三角形ABC中,AC= ![]() =
= ![]() ,
,
∴DG=3 ![]() +
+ ![]() ,BG=x﹣3,
,BG=x﹣3,
在直角三角形BDG中,∵BG=DGtan30°,
∴x﹣3=(3 ![]() +
+ ![]() )
) ![]()
解得:x≈13,
∴大树的高度为:13米.
【解析】根据解直角三角形中的实际应用,通过做辅助线,得到四边形DHCG为矩形,在直角三角形AHD中,由∠DAH=30°,AD=6,得到DH=3,AH=3 ![]() ,求出CG=3,在直角三角形ABC中,根据解直角三角形得到AC=
,求出CG=3,在直角三角形ABC中,根据解直角三角形得到AC= ![]() ,得到DG=3
,得到DG=3 ![]() +
+ ![]() ,BG=x﹣3,在直角三角形BDG中,由BG=DGtan30°,求出x的值即可.
,BG=x﹣3,在直角三角形BDG中,由BG=DGtan30°,求出x的值即可.
【考点精析】解答此题的关键在于理解关于仰角俯角问题的相关知识,掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目