题目内容
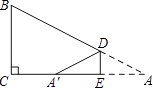
【题目】已知:如图∠1=∠2,∠3=∠4,∠5=∠6,∠1=60°,∠7=20°
(1)试说明AC⊥BD
(2)求∠3及∠5的度数
(3)求四边形ABCD各内角的度数.

【答案】(1)见解析;(2)30°,70°;(3)∠DAB =60°,∠ABC =80°,∠DCB =140°,∠ADC =80°
【解析】
(1)根据三角形内角和定理即可证得∠1+∠3=90°,则在△AOD中,利用内角和定理即可求得∠AOD=90°,即可证得;
(2)根据直角三角形的两个锐角互余即可求解;
(3)根据根据(2)即可求得∠DAB,∠ADC,∠DCB的度数,然后根据四边形的内角和定理即可求得∠ABC的度数.
(1)∵∠1+∠2+∠DAB=180°,
即∠1+∠2+∠3+∠4=180°,
又∵∠1=∠2,∠3=∠4,
∴∠1+∠3=90°,
∵∠1+∠3+∠AOD=90°,
∴∠AOD=90°,
∴AC⊥BD;
(2)∵∠1+∠3=90°,
∴∠3=90°∠1=90°60°=30°.
∵AC⊥BD,
∴∠COD=90°,
∴∠5+∠7=90°,
∴∠5=90°∠7=70°;
(3)∠DAB=2∠3=60°,
∠ADC=∠1+∠7=60°+20°=80°,
∠DCB=∠5+∠6=70°+70°=140°,
则∠ABC=360°∠DAB∠ADC∠DCB=80°.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目