题目内容
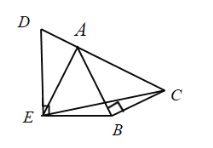
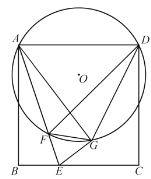
【题目】在正方形ABCD中,点E是BC边上一动点,连接AE,沿AE将△ABE翻折得△AGE,连接DG,作△AGD的外接⊙O,⊙O交AE于点F,连接FG、FD.
(1)求证∠AGD=∠EFG;
(2)求证△ADF∽△EGF;
(3)若AB=3,BE=1,求⊙O的半径.
【答案】(1)见解析;(2)见解析;(3)⊙O的半径为![]()
【解析】
(1)根据题目图形可知,本题考查圆内接四边形的性质应用,可利用对角互补解题;同时根据题干“翻折”信息可推出边等、角等信息,结合正方形ABCD边等性质即可解答;
(2)本题需以第一问结论作为角互换的桥梁,同时考查正方形ABCD性质,利用其平行特征推出角等,结合“翻折”图形性质进行角的互换,利用“角角”判定三角形相似;
(3)本题考查正方形以及圆的综合运用,借助正方形内角90°为媒介考查圆周角定理的运用,同时需要观察图形特点构造全等三角形,结合勾股定理求解边长.
(1)证明:∵四边形AFGD是⊙O的内接四边形,
∴∠ADG+∠AFG=180°,
∵∠AFG+∠EFG=180°,
∴∠ADG=∠EFG,
由正方形ABCD及翻折可得AB=AG=AD,
∴∠ADG=∠AGD,
∴∠AGD=∠EFG.
(2)∵∠AGD=∠AFD,∠AGD=∠EFG,
∴∠AFD=∠EFG,
∵四边形ABCD是正方形,
∴AD∥BC.
∴∠DAF=∠AEB.
由翻折得∠AEB=∠GEF,
∴∠DAF=∠GEF,
∴△ADF∽△EGF.
(3)解:设⊙O与CD交于点H,连接AH、GH,如下图所示
∵∠ADH=90°,
∴AH是⊙O的直径,
∴∠AGH=90°,
由翻折得∠AGE=90°,则∠AGE+∠AGH=180°,
∴E、G、H三点在一条直线上.
∵AH=AH,AD=AG,∴Rt△ADH≌Rt△AGH,∴GH=DH,
设GH=DH=x,则在Rt△ECH中,CH=3-x,EH=1+x,EC=3-1=2,
由CH2+EC2=EH2,即(3-x)2+22=(1+x)2,解得x=![]() ,
,
在Rt△ADH中,AD2+DH2=AH2,即32+(![]() )2=AH2,解得AH=
)2=AH2,解得AH=![]() ,
,
∴⊙O的半径为![]()


 名校课堂系列答案
名校课堂系列答案【题目】港珠澳大桥(英文名称:Hong Kong-Zhuhai-Macao Bridge)是中国境内一座连接香港、广东珠海和澳门的桥隧工程,位于中国广东省珠江口伶洋海域内,为珠江三角洲地区环线高速公路南环段.港珠澳大桥于![]() 年
年![]() 月
月![]() 日动工建设;于
日动工建设;于![]() 年
年![]() 月
月![]() 日实现主体工程全线贯通;于
日实现主体工程全线贯通;于![]() 年
年![]() 月
月![]() 日完成主体工程验收;同年
日完成主体工程验收;同年![]() 月
月![]() 日上午
日上午![]() 时开通运营.广东某校数学“综合与实践”小组的同学把“测量港珠澳大桥某一段斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间完成该桥斜拉索实地测量,测量结果如下表
时开通运营.广东某校数学“综合与实践”小组的同学把“测量港珠澳大桥某一段斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间完成该桥斜拉索实地测量,测量结果如下表
项目 | 内容 | ||
课题 | 测量港珠澳大桥某一段斜拉索顶端到桥面的距离 | ||
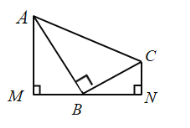
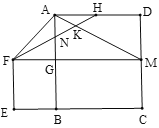
测量示意图 |
| 说明:两侧斜拉索 | |
测量数据 |
|
|
|
|
|
| |
|
| ||

(1)请帮助该小组根据上表中的测量数据,求斜拉索顶端点![]() 到
到![]() 的距离(参考数据:
的距离(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
(2)该小组要写出一份完整的课题活动报告,除上表的项目外,你认为还需要补充哪些项目(写出一个即可)?
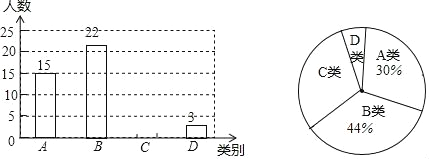
【题目】为了解九年级女生体质健康变化的情况,体育李老师本学期从九年级全体240名女生中随机抽取20名女生进行体质测试,并调取这20名女生上学期的体质测试成绩进行对比,李老师对两次数据(成绩)进行整理、描述和分析.下面给出了部分信息.
a. 两次测试成绩(百分制)的频数分布直方图如下(数据分组:60≤x<70,70≤x<80,80≤x<90,90≤x≤100):
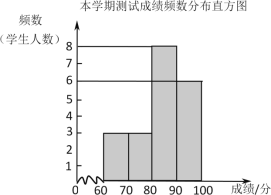
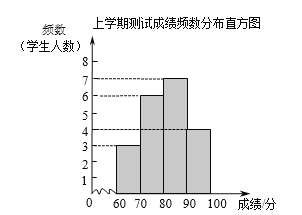
b.成绩在80≤x<90的是:
上学期:80 81 85 85 85 86 88
本学期:80 82 83 86 86 86 88 89
c. 两个学期样本测试成绩的平均数、中位数、众数如下:
学期 | 平均数 | 中位数 | 众数 |
上学期 | 84 | a | 85 |
本学期 | b | c | d |
根据以上信息,回答下列问题:
(1)表中a的值是 ;
(2)下列关于本学期样本测试成绩的结论:①c=86;②d=86;③成绩的极差可能为41;④b有可能等于80.其中所有正确结论的序号是 ;
(3)从两个不同角度分析这20名女生从上学期到本学期体质健康变化情况.