��Ŀ����
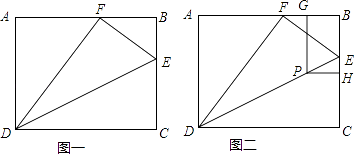
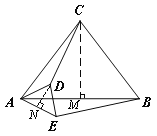
����Ŀ������ABC�У�CA��CB������AED�У� DA��DE����D��E�ֱ���CA��AB�ϣ�
��1����ͼ�٣�����ACB����ADE��90������CD��BE��������ϵ�� ��
��2������ACB����ADE��120��������AED�Ƶ�A��ת����ͼ����ʾ��λ�ã���CD��BE��������ϵ��
��3������ACB����ADE��2����0��< �� < 90����������AED�Ƶ�A��ת����ͼ����ʾ��λ�ã�̽���߶�CD��BE��������ϵ��������֤��(�ú�����ʽ�ӱ�ʾ)��
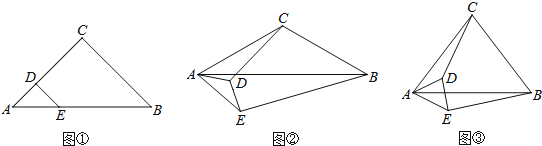
���𰸡���1��BE��![]() CD����2��BE��
CD����2��BE��![]() CD����3��BE=2CD��sin����֤����������
CD����3��BE=2CD��sin����֤����������
�������������������1������֪����ADE����ACB���ǵ���ֱ�������Σ�������AE=![]() AD��AB=
AD��AB=![]() AC���Ӷ���
AC���Ӷ���![]() ����BE��
����BE��![]() CD.
CD.
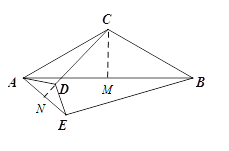
��2����ͼ���ֱ����C��D��CM��AB�ڵ�M��DN��AE�ڵ�N��
��CA��CB��DA��DE����ACB����ADE=120����
���CAB����DAE����ACM����ADN="60��" ��AM=![]() AB��AN=
AB��AN=![]() AE��
AE��
���CAD����BAE��
��Rt��ACM��Rt��ADN��sin��ACM=![]() =
=![]() ��sin��ADN=
��sin��ADN=![]() =
=![]() ��
��
��![]() ����
����![]() ��
��
���ߡ�CAD����BAE�����BAE�ס�CAD����![]() .��BE��
.��BE��![]() CD��
CD��
��3�����ݵ��������ε����ʺ�������Ǻ����������![]() ��������BAE�ס�CAD�ó�
��������BAE�ס�CAD�ó�![]() ���Ӷ��ó�����.
���Ӷ��ó�����.
��1��BE��![]() CD.
CD.
��2��BE��![]() CD.
CD.
��3��BE=2CD��sin����֤�����£�
��ͼ���ֱ����C��D��CM��AB�ڵ�M��DN��AE�ڵ�N��
��CA��CB��DA��DE����ACB����ADE="2��" ��
���CAB����DAE����ACM����ADN="��" ��AM=![]() AB��AN=
AB��AN=![]() AE��
AE��
���CAD����BAE��
��Rt��ACM��Rt��ADN��sin��ACM=![]() ��sin��ADN=
��sin��ADN=![]() ��
��
��![]() ����
����![]() ��
��
���ߡ�CAD����BAE�����BAE�ס�CAD����![]() .
.
��BE=2DC��sin����

����Ŀ��ij��Ʒÿ���ɱ�10Ԫ��������ÿ����Ʒ�����ۼ�x��Ԫ�����Ʒ����������y������֮��Ĺ�ϵ���±���
x ��Ԫ�� | 15 | 20 | 25 | �� |
y ������ | 25 | 20 | 15 | �� |
����������y�����ۼ�x��һ�κ�����
��1�������������y�����������ۼ�x��Ԫ���ĺ�����ϵʽ��
��2�������ۼ۶�Ϊ30Ԫʱ��ÿ�յ���������