题目内容
【题目】如图一,矩形ABCD中,AB=5cm,BC=4cm,E是BC上一点,将△CDE沿DE折叠,使点C落在AB上一点F处,连结DF、EF. 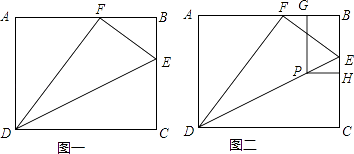
(1)求BE的长度;
(2)设点P、H、G分别在线段DE、BC、BA上,当BP=CP且四边形BGPH为矩形时,请说明矩形BGPH的长宽比为2:1,并求PE的长.(如图二)
【答案】
(1)解:如图一,
在矩形ABCD中,AD=BC=4,CD=AB=5,∠A=90°,
由折叠可得:DF=DC=5,CE=CF,
∴直角三角形ADF中,AF= ![]() =3,
=3,
∴BF=5=3=2,
设BE=x,则CE=FE=4﹣x,
在Rt△BEF中,22+x2=(4﹣x)2,
解得x=1.5,
即BE=1.5
(2)解:如图二,当BP=CP,且四边形BGPH为矩形时,点P在BC的垂直平分线上,
即PH垂直平分BC,
∴BH=CH= ![]() BC=2,①
BC=2,①
又∵BE=1.5,
∴EH=0.5,EC=2.5
∵PH∥DC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]()
解得PH=1,②
∴由①②得:矩形BGPH的长宽比为2:1,
在Rt△PEH中,PE= ![]() =
= ![]() =
= ![]()
【解析】(1)先根据矩形性质以及折叠变换,运用勾股定理求得AF、BF的长,再设BE=x,在Rt△BEF中运用勾股定理列出方程,求得x的值.(2)先判断PH垂直平分BC,求得矩形中BH的长,再根据平行线分线段成比例定理,求得PH的长,进而得出矩形BGPH的长宽比为2:1,最后根据勾股定理求得PE的长.
【考点精析】利用勾股定理的概念和矩形的性质对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目