Question

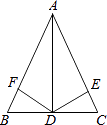
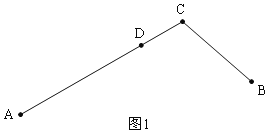
【题目】如果一点在由两条公共端点的线段组成的一条折线上且把这条折线分成长度相等的两部分，这点叫做这条折线的“折中点”．如图，点D是折线A﹣C﹣B的“折中点”，请解答以下问题：

（1）当AC＞BC时，点D在线段　 上； 当AC＝BC时，点D与　 　重合；当AC＜BC时，点D在线段　 　上；

（2）若AC＝18cm,BC＝10cm,若∠ACB=90°,有一动点P从C点出发，在线段CB上向点B运动，速度为2cm/s, 设运动时间是t（s）, 求当t为何值，三角形PCD 的面积为10？

（3）若E为线段AC中点，EC＝8cm，CD＝6cm，求CB的长度．

Answer 1

【答案】（1）AC，C，BC； (2) s；（3）CB的长度是4cm或28cm.

【解析】试题分析：（1）根据图形以及阅读材料所给的信息直接填空即可；(2)如图4，先表示PC=2t，由折中点的定义得AD=14，根据三角形的面积公式列式可求t的值；（3）分当点D在线段AC上与BC上两种情况求解即可.

试题解析：

(1)当AC>BC时，如图1，点D在线段AC上；

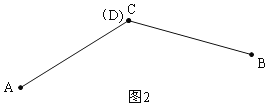
当AC=BC时，如图2，点D与C重合；

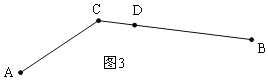
当AC<BC时，如图3，点D在线段BC上；

因此，本题正确答案是：AC，C，BC.

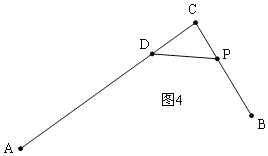
（2）如图4，根据题意得：PC=2t，

∵AC=18，BC=10 cm，

∴AC+BC=18+10=28 cm，

∵D点是折中点，

∴AD=14cm，

∴CD=18-14=4cm，

∵∠ACB=90°，

∴，

即，

解得，

则当t为秒时，三角形PCD的面积为10cm2；

(3)分两种情况：

①点D在线段AC上时，如图5，

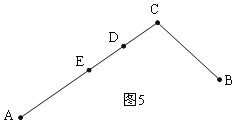
∵E为线段AC中点,EC=8 cm,

∴AC=2CE=16cm，

∵CD=6cm，

∴AD=AC-CD=16-6=10cm，

∵D为折中点，

∴AD=CD+BC，

∴BC=AD-CD=10-6=4cm；

②点D在线段BC上,如图6,

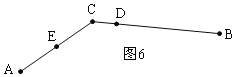
∵E为线段AC中点，EC=8cm，

∴AC=2CE=16cm，

∴AD=AC+CD=16+6=22cm，

∴BD=AC+CD=22cm，

∴BC=BD+CD=22+6=28cm.

综上所述，CB的长度是4 cm 或28 cm.