题目内容
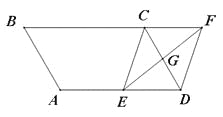
【题目】如图1,矩形ABCD中,AB=6,BC=8,点E、F分别是BC、CD边上的点,且AE⊥EF,BE=2,
(1)求证:AE=EF;
(2)延长EF交矩形∠BCD的外角平分线CP于点P(图2),试求AE与EP的数量关系;

【答案】(1)见解析;(2) AE=![]() EP.
EP.
【解析】分析:(1)通过证明△ABE≌△ECF即可得出结论;
(2)在AB上取一点M,使BM=BE,连接ME,通过证明△AME∽△ECP即可求得结论.
详解:(1)∵AE⊥EF,
∴∠BEA+∠CEF=90°,
∵四边形ABCD为矩形,
∴∠B=∠C=90°,
∴∠BAE +∠BEA =90°,
∴∠BA E=∠CEF,
又∵AB=DC=6,BC=8,BE=2,
∴AB=EC=6,
∴△ABE≌△ECF(ASA),
∴AE=EF.
(2)如图,在AB上取一点M,使BM=BE,连接ME.
∴AM=CE,
∴∠BME=45°,
∴∠AME=135°,
∵CP是外角平分线,
∴∠DCP=45°,
∴∠ECP=135°,
∴∠AME=∠ECP,
由(1)知∠MA E=∠CEP, ∴△AME∽△ECP.
∴![]() ,
,
∵AM=2,EC=3,
∴![]() ,
,
∴AE与EP的数量关系:AE=![]() EP.
EP.

【题目】恰逢“植树节”,师梅与博小两所学校决定购进A,B两种树苗进行种植,已知两所学校共花费了390元购进了50棵树苗,其中A树苗10元一棵,B树苗5元一棵.现在要将50棵树苗运往两所学校,其运费如下表所示:
树苗类型 | 师梅(元/棵) | 博小(元/棵) |
A | 8 | 10 |
B | 6 | 5 |
(1)求这50棵树苗中A、B树苗各多少棵?
(2)现师梅需要30棵树苗,博小需要20棵树苗,设师梅需要A树苗为x棵,运往师梅和博小的总运费为y,求y与x的函数解析式.
(3)在(2)的条件下,若运往师梅的运费不超过200元,请你写出使总运费最少的树苗分配方案,并求出最少费用.