题目内容
【题目】台球桌的形状是一个长方形，当母球被击打后可能在不同的边上反弹，为了母球最终击中目标球，击球者需作出不同的设计，确定击球的方向，因此，台球既复杂又有趣，台球运动被称为智慧和技能的较量．
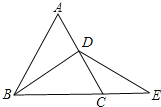
问题1：如图（1），如果母球P击中桌边点A，经桌边反弹击中相邻另一条桌边，再次反弹，那么母球P经过的路线BC与PA平行吗？证明你的判断．
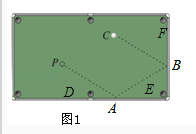
问题2：在一张简易球桌ABCD上，如图（2）所示，目标球F、母球E之间有一个G球阻挡，击球者想通过击打母球E先撞球台的CD边，过一次反弹后再撞击F球，他应将E球打到CD边上的哪一点？
请用尺规作图在图（2）中作出这一点．
问题3：如图（3），在简易球台ABCD上，已知AB=4，BC=3．母球P从角落A以45°角击出，在桌子边缘回弹若干次后，最终必将落入 （填A、B、C、D）角落的球袋，在它落入球袋之前，与桌子边缘共回弹了 次；若AB=100，BC=99，母球P还终将会落入某个角落的球袋，则它在落入球袋之前，在桌子边缘总共回弹了 次．
考点：作图—应用与设计作图．
【答案】问题1 BC∥PA；问题2见解析；问题3比前一次的位置下移2格，所以要撞击边的次数为100+99﹣2=197次．
【解析】
试题分析：（1）类似于光线的反射问题，可通过计算同旁内角互补，得出平行的结论；
（2）入射角等于反射角，找出E点关于AB的对称点E1，连接E1F交AB于H根据对称图形的特点及对顶角相等得出∠BHF=∠E1HA=∠EHA，求出E1N及NF的长运用勾股定理求出E1F的长，因对应边EH=E1H，E1H即为所求；
（3）根据当AB=4，AD=3时的例图及弹子的运行规律：每一条运行轨迹都是一个正方形的对角线，画出图形，即可得出结论．
解：（1）如图，
∵∠PAD=∠BAE，∠PAB=180°﹣∠PAD﹣∠BAE，
∴∠PAB=180°﹣2∠BAE．
同理，∠ABC=180°﹣2∠ABE．
∵∠BAE+∠ABE=90°，
∴∠PAB+∠ABC=360°﹣2（∠BAE+∠ABE）=180°．
∴BC∥PA．
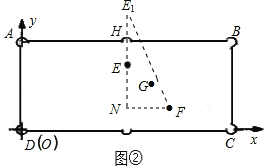
（2）可作点E关于直线AB的对称点E1，连接E1F，E1F与AB交于点H，球E的运动路线就是EH→HF，
过点F作AB的平行线交E1E的延长线于点N，
；
（3）如图，
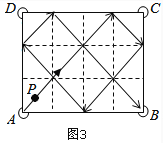
母球P从角落A以45°角击出，在桌子边缘回弹若干次后，最终必将落入B（填A、B、C、D）角落的球袋，在它落入球袋之前，与桌子边缘共回弹了5次；
设由DC边反弹，弹子撞击BC边的位置距离C点为K格，从BC边反弹后，弹子撞击AB边的位置距离B点为（99﹣k）格，距离A点为（k+1）格经过AB边反弹后，弹子撞击AD边的位置距离A点为（k+1）格，距离D点为[99﹣（K+1）]格，经AD反弹，弹子撞击DC边的位置距离D点为[99﹣（k+1）]格，距离C点为100﹣[99﹣（K+1）]=K+2格再撞击BC边的位置距离C点为k+2格，即比前一次的位置下移2格，所以要撞击边的次数为100+99﹣2=197次．
