Question

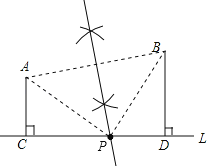
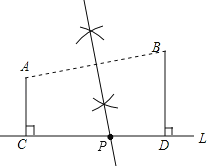
【题目】如图，在笔直的公路L的同侧有A、B两个村庄，已知A、B两村分别到公路的距离AC=3km，BD=4km．现要在公路上建一个汽车站P，使该车站到A、B两村的距离相等，

（1）试用直尺和圆规在图中作出点P；（保留作图痕迹）

（2）若连接AP、BP，测得∠APB=90°，求A村到车站的距离．

Answer 1

【答案】（1）作图见解析；（2）A村到车站的距离5km．

【解析】

试题分析：（1）连接AB，作AB的垂直平分线与AB交于点P即可；

（2）先利用AAS证明△ACP≌△PDB，得出CP=BD=4km，然后在Rt△ACP中利用勾股定理求出AP2=AC2+CP2=32+42=25，则AP=5．

解：（1）连结AB，画出AB的垂直平分线交CD于P，

则点P即为所求的点；

（2）∵∠APB=90°，

∴∠APC+∠BPD=90°，

又∵∠APC+∠CAP=90°，

∴∠CAP=∠BPD，

又∵∠ACP=∠PDB=90°，

∵MN垂直平分AB，

∴AP=BP，

∴△ACP≌△PDB（AAS），

∴CP=BD=4km，

在Rt△ACP中，∠ACP=90°，

AP2=AC2+CP2=32+42=25，

∴AP=5．

答：A村到车站的距离5km．