Question

【题目】如图，在等边三角形ABC中，BD是AC边上的中线，延长BC到E，使CE=CD．

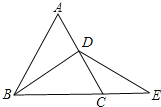
问：

（1）DB与DE相等吗？

（2）把BD是AC边上的中线改成什么条件，还能得到同样的结论？

Answer 1

【答案】（1）相等，理由见解析；（2）把BD是AC边上的中线改为BD是∠ABC的平分线或BD是AC边上的高，根据等边三角形“三线合一”的性质，还能得出DB=DE．

【解析】

试题分析：（1）由CD=CE，得到∠E=∠EDC，由于∠ACB=60°，求得∠E=30°，于是得到∠E=∠DBC，根据等腰三角形的判定即可得到结论；

（2）根据等边三角形“三线合一”的性质，即可得到结论．

解：（1）相等，

理由：∵CD=CE，

∴∠E=∠EDC，

又∵∠ACB=60°，

∴∠E=30°，

又∵∠DBC=30°，

∴∠E=∠DBC，

∴DB=DE；

（2）把BD是AC边上的中线改为BD是∠ABC的平分线或BD是AC边上的高，根据等边三角形“三线合一”的性质，还能得出DB=DE．