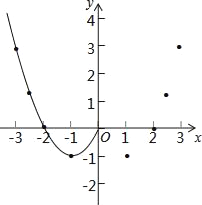题目内容
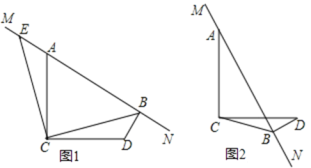
【题目】如图，已知△ABC在平面直角坐标系中的位置如图所示，
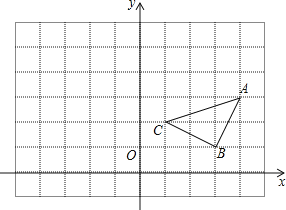
（1）写出△ABC三个顶点的坐标；
（2）求出△ABC的面积；
（3）在图中画出把△ABC先向左平移5个单位，再向上平移2个单位后所得的△A′B′C′，并写出各顶点坐标．
【答案】（1）A（4，3）、B（3，1）、C（1，2）；（2）△ABC的面积为
；（3）如图所示，见解析；△A′B′C′即为所求，A′（﹣1，5）、B′（﹣2，3）、C′（﹣4，4）．
【解析】
（1）由△ABC在平面直角坐标系中的位置可得答案；
（2）利用割补法求解可得答案；
（3）将三个顶点分别向左平移5个单位，再向上平移2个单位得到对应点，继而首尾顺次连接即可得．
解：（1）A（4，3）、B（3，1）、C（1，2）；
（2）△ABC的面积为2×3﹣
×1×2×2﹣×1×3＝；
（3）如图所示，△A′B′C′即为所求，
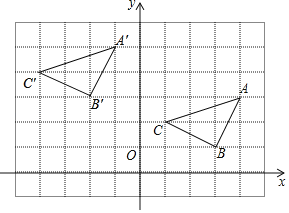
由图知A′（﹣1，5）、B′（﹣2，3）、C′（﹣4，4）．
练习册系列答案
阅读快车系列答案
相关题目
【题目】在数学拓展课上，九（1）班同学根据学习函数的经验，对新函数y=x2﹣2|x|的图象和性质进行了探究，探究过程如下：
【初步尝试】求二次函数y=x2﹣2x的顶点坐标及与x轴的交点坐标；
【类比探究】当函数y=x2﹣2|x|时，自变量x的取值范围是全体实数，下表为y与x的几组对应值．
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| 0 | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
①根据表中数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请你画出该函数图象的另一部分；
②根据画出的函数图象，写出该函数的两条性质．
【深入探究】若点M（m，y1）在图象上，且y1≤0，若点N（m+k，y2）也在图象上，且满足y2≥3恒成立，求k的取值范围．
