题目内容
【题目】对于平面直角坐标系xOy中的点和⊙O，给出如下定义：过点A的直线l交⊙O于B，C两点，且A、B、C三点不重合，若在A、B、C三点中，存在位于中间的点恰为以另外两点为端点线段的中点时，则称点A为⊙O的价值点．
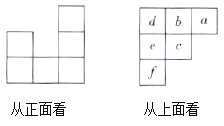
（1）如图1，当⊙O的半径为1时．
①分别判断在点D（
，），E（﹣1，
），F（2，3）中，是⊙O的价值点有 ；
②若点P是⊙O的价值点，点P的坐标为（x，0），且x＞0，则x的最大值为 ．
（2）如图2，直线y=﹣
x+3与x轴，y轴分别交于M、N两点，⊙O半径为1，直线MN上是否存在⊙O的价值点？若存在，求出这些点的横坐标的取值范围，若不存在，请说明理由；
（3）如图3，直线y=﹣x+2与x轴、y轴分别交于G、H两点，⊙C的半径为1，且⊙C在x轴上滑动，若线段GH上存在⊙C的价值点P，求出圆心C的横坐标的取值范围．
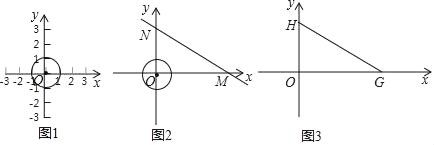
【答案】（1）①D，E；②3；（2）0≤x≤
；（3） 0≤x≤9．
练习册系列答案
相关题目
