题目内容
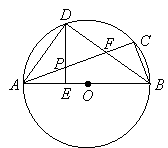
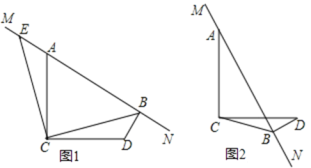
【题目】已知∠ACD=90°,MN是过A点的直线,AC=DC,DB⊥MN于点B,连接BC.
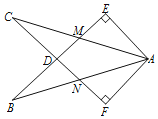
(1)如图1,将△BCD绕点C逆时针方向旋转90°得到△ECA.
①求证:点E在直线MN上;
②猜想线段AB、BD、CB满足怎样的数量关系,并证明你的猜想.
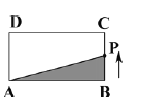
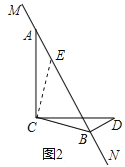
(2)当MN绕点A旋转到如图2的位置时,猜想线段AB、BD、CB又满足怎样的数列关系,并证明你的猜想.
【答案】(1)①见解析;②AB+BD=![]() BC,理由见解析;(2)ABBD=
BC,理由见解析;(2)ABBD=![]() BC,理由见解析;
BC,理由见解析;
【解析】
(1)①由四边形内角和定理得出∠CAB+∠CDB=180°,由旋转的性质得出△ECA≌△BCD,得出∠EAC=∠BDC,因此∠CAB+∠EAC=180°,即可得出结论;
②证出△ECB为等腰直角三角形,由勾股定理得出BE=![]() BC,再由BE=AE+AB,AE=BD,即可得出结论;
BC,再由BE=AE+AB,AE=BD,即可得出结论;
(2)过点C作CE⊥CB与MN交于点E,则∠ECB=90°,∠ACE=∠DCB,证出∠CAE=∠CDB,由ASA证明△ACE≌△DCB,得出AE=DB,EC=BC,证出△ECB为等腰直角三角形,由勾股定理得出EB=![]() BC,即可得出结论.
BC,即可得出结论.
(1)①证明:∵DB⊥MN,
∴∠ABD=90,在四边形ACDB中,
∵∠ACD=90
∴∠ACD+∠ABD=180
∴∠CAB+∠CDB=180
由旋转的性质得:△ECA≌△BCD
∴∠EAC=∠BDC,
∴∠CAB+∠EAC=180
∴点E在直线MN上
②解:AB+BD=![]() BC,理由如下:
BC,理由如下:
∵∠ACD=90
∴∠ACB+∠BCD=90
由①知∠ECA=∠BCD,EC=BC
∴∠ECB=∠ECA+∠ACB=90
∴△ECB为等腰直角三角形
∴BE=![]() BC
BC
∵BE=AE+AB
由①知AE=BD
∴AB+BD=![]() BC.
BC.
(2)解:ABBD=![]() BC,理由如下:
BC,理由如下:
过点C作CE⊥CB与MN交于点E,如图2所示:
则∠ECB=90
∵∠ACD=90
∴∠ACE=∠DCB
∵DB⊥AB
∴∠CAE=∠CDB
∴△ACE≌△DCB(ASA)
∴AE=DB,EC=BC
∴EB=ABAE=ABDB,△ECB为等腰直角三角形,
∴EB=![]() BC
BC
∴ABBD=![]() BC.
BC.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案