题目内容
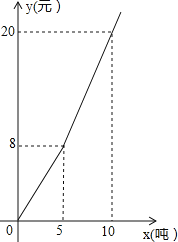
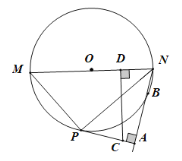
【题目】如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG、BG、DG,下列结论中错误的是( )
A.BC=DFB.△DCG≌△BGCC.△DFG≌△BCGD.AC:BG=![]() :1
:1
【答案】B
【解析】
A选项,根据矩形的性质得:BC=AD,∠BAD=∠ADC=90°,由角平分线可得△ADF是等腰直角三角形,则BC=DF=AD;
B选项,证明△DCG≌△BEG,可作判断;
C选项,根据等腰三角形的性质得:∠AFD=∠FCG=45°,根据SAS可证明△DGF≌△BGC;
D选项,连接BD,先根据矩形的对角线相等得:AC=BD,根据以上证得:△DCG≌△BEG,得DG=BG,∠CGD=∠EGB,得△DGB是等腰直角三角形,根据勾股定理可得结论.
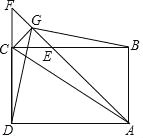
解:A选项,∵四边形ABCD是矩形,
∴BC=AD,∠BAD=∠ADC=90°,
∵AF平分∠BAD,
∴∠BAE=∠DAF=45°,
∴△ADF是等腰直角三角形,
∴DF=AD,
∴BC=DF,
故选项A正确;
B选项,Rt△EFC中,∵G是EF的中点,
∴CG=FG=EG,
∵∠CEF=∠FCG=45°,
∴∠BEG=∠DCG,
∵BE=CD,
∴△DCG≌△BEG,
故选项B错误;
C选项,∵FG=CG,
∴∠AFD=∠FCG=45°,
∵∠BCF=90°,
∴∠BCG=45°,
∴∠BCG=∠DFG,
∵BC=DF,
∴△DGF≌△BGC,
故选顶C正确;
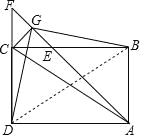
D选项,连接BD,∵四边形ABCD是矩形,
∴AC=BD,
∵△DCG≌△BEG,
∴DG=BG,∠CGD=∠EGB,
∴∠CGD+∠AGD=∠EGB+∠AGD=90°,
∴△DGB是等腰直角三角形,
∴BD=![]() BG,
BG,
∴AC=![]() BG,
BG,
∴AC:BG=![]() :1,
:1,
故选项D正确;
本题选择结论中错误的选项,
故选B.

【题目】某公司为了宣传一种新产品,在某地先后举行![]() 场产品促销会,已知该产品每台成本为
场产品促销会,已知该产品每台成本为![]() 万元,设第
万元,设第![]() 场产品的销售量为
场产品的销售量为![]() (台),在销售过程中获得以下信息:
(台),在销售过程中获得以下信息:
信息1:已知第一场销售产品![]() 台,然后每增加一场,产品就少卖出
台,然后每增加一场,产品就少卖出![]() 台;
台;
信息2:产品的每场销售单价![]() (万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场--第20场浮动价与销售场次
(万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场--第20场浮动价与销售场次![]() 成正比,第21场--第40场浮动价与销售场次
成正比,第21场--第40场浮动价与销售场次![]() 成反比,经过统计,得到如下数据:
成反比,经过统计,得到如下数据:
| 3 | 10 | 25 |
| 10.6 | 12 | 14.2 |
(1)求![]() 与
与![]() 之间满足的函数关系式;
之间满足的函数关系式;
(2)当产品销售单价为13万元时,求销售场次是第几场?
(3)在这![]() 场产品促销会中,哪一场获得的利润最大,最大利润是多少?
场产品促销会中,哪一场获得的利润最大,最大利润是多少?