题目内容
【题目】如图,在锐角△ABC中,AB=2,AC=![]() ,∠ACB=45°,D是平面内一点且∠ADB=30°,则线段CD的最小值为_____.
,∠ACB=45°,D是平面内一点且∠ADB=30°,则线段CD的最小值为_____.
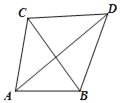
【答案】3﹣![]()
【解析】
作AH⊥BC于H,因为AB=2,AC=![]() ,∠ACB=45°,可得∠ABH=60°,BC=
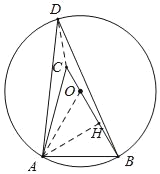
,∠ACB=45°,可得∠ABH=60°,BC=![]() +1,在BC上截取BO=AB=2,则△OAB为等边三角形,以O为圆心,2为半径作⊙O,根据∠ADB=30°,可得点D在⊙O上运动,当DB经过圆心O时,CD最小,其最小值为⊙O的直径减去BC的长.
+1,在BC上截取BO=AB=2,则△OAB为等边三角形,以O为圆心,2为半径作⊙O,根据∠ADB=30°,可得点D在⊙O上运动,当DB经过圆心O时,CD最小,其最小值为⊙O的直径减去BC的长.
如图,作AH⊥BC于H,
∵AB=2,AC=![]() ,∠ACB=45°,
,∠ACB=45°,
∴CH=AH=![]() ,
,
∴BH=![]() ,
,
∴∠ABH=60°,BC=CH+BH=![]() ,
,
在BC上截取BO=AB=2,则△OAB为等边三角形,
以O为圆心,2为半径作⊙O,
∵∠ADB=30°,
∴点D在⊙O上运动,
当DB经过圆心O时,CD最小,
最小值为4﹣(![]() +1)=3﹣
+1)=3﹣![]() .
.
故答案为:3﹣![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目