��Ŀ����
����Ŀ��x2+(p+q)x+pq��ʽ������ѧѧϰ�г�����һ�����ʽ����ν��������͵�ʽ����ʽ�ֽ��أ���Ϊ(x+p)(x+q)= x2+(p+q)x+pq�����ԣ�������ʽ�ֽ�������ʽ�˷������෴�ı��Σ��������ֹ�ϵ�ɵã�x2+(p+q)x+pq=(x+p)(x+q).�磺x2+3x+2=x2+(1+2)x+1��2=(x+1)(x+2)���������̻������������ʮ����˵���ʽ��ʾ:�ȷֽ������ϵ�����ֱ�д��ʮ�ֽ����ߵ����ϽǺ����½ǣ��ٷֽⳣ����ֱ�д��ʮ�ֽ����ߵ����ϽǺ����½ǣ�Ȼ����ˣ�������ͣ�ʹ�����һ�����ϵ��������ͼ.���������ǿ��Եõ���x2+3x+2= (x+1)(x+2)���������ַ����������ж���ʽ�ֽ���ʽ��
��1��x2+7x+10
��2����2x2��6x+36

���𰸡���1��![]() ����2��
����2��![]()
��������
��1���ȰѶ�����ϵ���ֽ�1��1���ѳ�����Ҳ�ֳ�2��5���ѶԽ����ϵ�������������ˣ��ٽ����õĻ���ӣ�ǡ�õ���һ����ϵ��7��
��2���ȰѶ�����ϵ���ֽ�1��-2���ѳ�����Ҳ�ֳ�6��6���ѶԽ����ϵ�������������ˣ��ٽ����õĻ���ӣ�ǡ�õ���һ����ϵ��-6.
��1��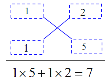
��![]()
��1��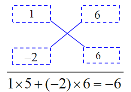
��![]()

��ϰ��ϵ�д�
�����Ŀ