题目内容
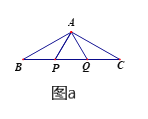
【题目】如图a,P、Q是△ABC的边BC上的两点,且△APQ为等边三角形,AB=AC,
(1)求证:BP=CQ.
(2)如图a,若∠BAC=120![]() ,AP=3,求BC的长.
,AP=3,求BC的长.
(3)若∠BAC=120![]() ,沿直线BC向右平行移动△APQ得到△A′P′Q′(如图b),A′Q′与AC交于点M.当点P移动到何处时,△AA′M≌△CQ′M?证明你的结论.
,沿直线BC向右平行移动△APQ得到△A′P′Q′(如图b),A′Q′与AC交于点M.当点P移动到何处时,△AA′M≌△CQ′M?证明你的结论.

【答案】(1)证明见解析;(2)9;(3)当点P移动到BC的中点时,△AA′M≌△CQ′M,证明见解析.
【解析】
(1)根据AB=AC,△APQ为等边三角形,利用AAS证得![]() ,从而证得结论;
,从而证得结论;
(2)根据AB=AC,∠BAC=120![]() ,得∠B=∠C=30
,得∠B=∠C=30![]() ,根据△APQ为等边三角形结合外角定理,∠BAP =∠B=∠C=∠CAQ=30
,根据△APQ为等边三角形结合外角定理,∠BAP =∠B=∠C=∠CAQ=30![]() ,继而求得答案;
,继而求得答案;
(3)根据平移的性质结合平行线的性质,即可得到答案.
(1)∵AB=AC,∴∠B=∠C
∵△APQ为等边三角形,
∴AP=AQ,∠APQ=∠AQP
∴∠APB=∠AQC
∴![]()
∴BP=CQ
(2)在△ABC中,AB=AC,∠BAC=120![]()
∴∠B=∠C=30![]()
已知△APQ为等边三角形,∴∠APQ=∠AQP=60![]()
∴∠BAP =∠B=∠C=∠CAQ=30![]()
∴AP=BP,AQ=CQ,
已知△APQ为等边三角形
∴BP=PQ=QC=AP=3
∴BC=9.
(3)当点P移动到BC的中点,即,P′为BC的中点时,
△AA′M≌△CQ′M.
证明:沿直线BC向右平行移动△APQ得到△A′P′Q′.
由平移的性质可知:PP'=AA'=QQ'.
AA'∥BC
∴∠C=∠MAA'①
当P′为BC的中点时,BP'=CP',由(2)的解答可知,PB=QC=PQ
∴BP'-PB=CP'-QC
∴PP'=AA'=QQ'= ![]() PQ=
PQ= ![]() QC
QC
∴点Q'为QC的中点.
Q'C=QQ'=AA'②
又∠AMA'=∠CMQ'③
∴由①②③可得△AA′M≌△CQ′M.

 阅读快车系列答案
阅读快车系列答案