题目内容
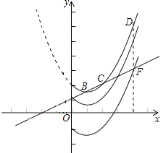
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,顶点为点
,顶点为点![]() ,点
,点![]() 与点
与点![]() 关于抛物线的对称轴对称.
关于抛物线的对称轴对称.

![]() 求直线
求直线![]() 的解析式;
的解析式;
![]() 点
点![]() 在抛物线上,且点
在抛物线上,且点![]() 的横坐标为
的横坐标为![]() .将抛物线在点
.将抛物线在点![]() ,
,![]() 之间的部分(包含点
之间的部分(包含点![]() ,
,![]() )记为图象
)记为图象![]() ,若图象
,若图象![]() 向下平移
向下平移![]() 个单位后与直线
个单位后与直线![]() 只有一个公共点,求
只有一个公共点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)欲求直线BC的解析式,需要求得点B、C的坐标,由抛物线解析式求得点A、B的坐标,然后根据点的对称性得到点C的坐标,然后由待定系数法来求直线方程;(2)根据抛物线解析式![]() 易求D(4,6),由直线
易求D(4,6),由直线![]() 易求点(0,1),点F(4,3),设点A平移后的对应点为点A',点D平移后的对应点为点D',当图象G向下平移至点
易求点(0,1),点F(4,3),设点A平移后的对应点为点A',点D平移后的对应点为点D',当图象G向下平移至点
A'与点E重合时,点D'在直线BC上方,此时t=1,当图象G向下平移至点D'与点F重合时,点A'在直线BC下方,此时t=3,结合图象可以知道,符合题意的t的取值范围是1<t≤3.
![]() ∵抛物线
∵抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
∵![]() ,
,
∴抛物线的对称轴为直线![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() .
.
又∵点![]() 与点
与点![]() 关于抛物线的对称轴对称,
关于抛物线的对称轴对称,
∴点![]() 的坐标为
的坐标为![]() ,且点
,且点![]() 在抛物线上.
在抛物线上.
设直线![]() 的解析式为
的解析式为![]() .
.
∵直线![]() 经过点
经过点![]() 和点
和点![]() ,
,
∴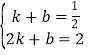 ,
,
解得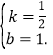
∴直线![]() 的解析式为:
的解析式为:![]() ;
;
![]() ∵抛物线
∵抛物线![]() 中,当
中,当![]() 时,
时,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
∵直线![]() 中,当
中,当![]() 时,
时,![]() .当
.当![]() 时,
时,![]() ,
,
∴如图,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
设点![]() 平移后的对应点为点
平移后的对应点为点![]() ,点
,点![]() 平移后的对应点为点
平移后的对应点为点![]() .当图象
.当图象![]() 向下平移至点
向下平移至点![]() 与点
与点![]() 重合时,点
重合时,点![]() 在直线
在直线![]() 上方,
上方,
此时![]() .
.
当图象![]() 向下平移至点
向下平移至点![]() 与点
与点![]() 重合时,点
重合时,点![]() 在直线
在直线![]() 下方,此时
下方,此时![]() .
.
结合图象可知,符合题意的![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目







