题目内容
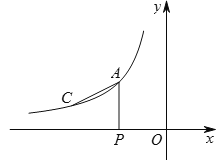
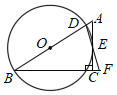
【题目】如图，在Rt△ABC中，∠ACB＝90°，点D是AB边上一点，以BD为直径的⊙O与边AC相切于点E，连接DE并延长DE交BC的延长线于点F．
（1）求证：BD＝BF；
（2）填空：
①若⊙O的半径为5，tanB＝
，则CF＝ ；
②若⊙O与BF相交于点H，当∠B的度数为 时，四边形OBHE为菱形．
【答案】（1）见解析；（2）①2；②60°
【解析】
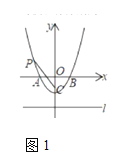
（1）如图1中，连接OE．利用三角形的中位线定理证明BF＝2OE，再根据BD＝2OE即可证明．
（2）①如图1中，想办法求出BC，BF即可解决问题．
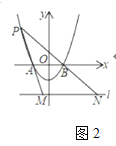
②结论：当∠B＝60°时，四边形BOEH是菱形．如图2中，连接OE，EH．首先证明OB∥EH，根据OE∥BC，推出四边形BOEH是平行四边形即可解决问题．
（1）证明：如图1中，连接OE．
∵AE是⊙O的切线，
∴OE⊥AC，
∴∠AEO＝∠ACB＝90°，
∴OE∥BC，
∵OB＝OD，
∴DE＝EF，
∴BF＝2OE，
∵BD＝2OE，
∴BD＝BF．
（2）①解：如图1中，由题意BD＝BF＝2OE＝10，
∵OE∥BC，
∴∠AOE＝∠B，
∴tan∠AOE＝tan∠B＝
∵OE＝5，
∴AE＝
，
∵AE2＝ADAB，
∴
＝AD（AD+10），
解得AD＝
或﹣
（舍弃）
∵∠ACB＝90°，设AC＝4k，BC＝3k，
则有（10+）2＝16k2+9k2，
解得k＝
或﹣（舍弃），
∴BC＝3k＝8，
∴CF＝BF﹣BC＝10﹣8＝2．
故答案为2．
②解：结论：当∠B＝60°时，四边形BOEH是菱形．
理由：如图2中，连接OE，EH．
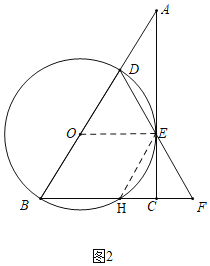
∵BD＝BF，∠B＝60°，
∴△BDC是等边三角形，
∴∠BDE＝60°，
∵∠BHE+∠BDE＝180°，
∴∠BHE＝120°，
∴∠B+∠BHE＝180°，
∴OB∥HE，
∵OE∥BH，
∴四边形BOEH是平行四边形，
∵OB＝OE，
∴四边形BOEH是菱形．
故答案为60°．
