题目内容
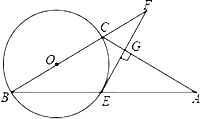
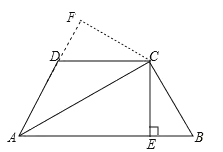
【题目】如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,AD+AB=2AE,
求证:∠ADC+∠B=180

【答案】见解析.
【解析】
延长AD过C作CF垂直AD于F,由条件可证△AFC≌△AEC,得到CF=CE.再由条件AD+AB=2AE可证BE=DF,所以△CDF≌△CEB,由全等的性质可得∠B=∠FDC,问题得证.
证明:延长AD过C作CF垂直AD于F,
∵AC平分∠BAD,
∴∠FAC=∠EAC,
∵CE⊥AB,CF⊥AD,
∴∠AFC=∠AEC=90°,AC=AC,
∴△AFC≌△AEC(AAS),
∴AF=AE,CF=CE,
∵AD+AB=2AE,
又∵AD=AFDF,AB=AE+BE,AF=AE,
∴2AE=AE+BE+AEDF,
∴BE=DF,
在△CDF和△CBE中,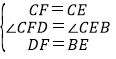 ,
,
∴△CDF≌△CBE(SAS),
∴∠B=∠FDC,
∵∠ADC+∠FDC=180°,
∴∠ADC+∠B=180.

练习册系列答案
相关题目