题目内容
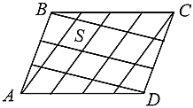
【题目】如图, 
ABCD中，EF⊥CD交BD于点G，∠ECF=∠DGF，DG=CE，求证：四边形ABCD是菱形．
【答案】证明见解析
【解析】
令AC与BD交于点K，利用AAS证出△CEF≌△GDF，从而得出∠CEF=∠GDF，即可得出∠DFG=∠AKD=90°，然后根据菱形的判定定理即可证出结论．
证明：令AC与BD交于点K．
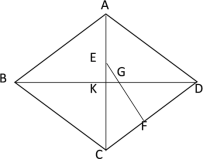
∵EF⊥CD
∴∠EFC=∠DFG=90°
∵DG=CE，∠ECF=∠DGF
∴△CEF≌△GDF（AAS）
∴∠CEF=∠GDF
∵∠EGB=∠DGF ，∠DFG=180°-∠DGF -∠DGF，∠AKD=180°-∠CEF-∠EGB
∴∠DFG=∠AKD=90°
即AC⊥BD
∵四边形ABCD为平行四边形
∴四边形ABCD为菱形
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
