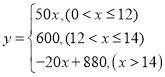题目内容
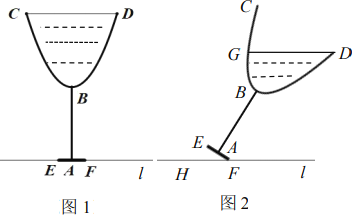
【题目】图1是一个高脚杯截面图,杯体![]() 呈抛物线状(杯体厚度不计),点
呈抛物线状(杯体厚度不计),点![]() 是抛物线的顶点,
是抛物线的顶点,![]() ,点
,点![]() 是
是![]() 的中点,当高脚杯中装满液体时,液面
的中点,当高脚杯中装满液体时,液面![]() ,此时最大深度(液面到最低点的距离)为
,此时最大深度(液面到最低点的距离)为![]() ,将高脚杯绕点
,将高脚杯绕点![]() 缓缓倾斜倒出部分液体,当
缓缓倾斜倒出部分液体,当![]() 时停止,此时液面为
时停止,此时液面为![]() ,则液面
,则液面![]() 到平面
到平面![]() 的距离是________________;此时杯体内液体的最大深度为_____________________.
的距离是________________;此时杯体内液体的最大深度为_____________________.
【答案】![]()
![]()
【解析】
作CD的垂线FG,DF绕F旋转后为FP,作PH垂直EF的延长线于H,利用三角函数和差公式计算出![]() ,从而求得
,从而求得![]() ,进而求解.
,进而求解.
建立直角坐标系,在DG下方的抛物线上任取一点Q,过点Q作y轴的平行线交DG于点P,过点Q作DG的垂线QM,垂足为M.求出直线DG及抛物线解析式,利用三角形DGQ的面积作为桥梁可求出QM的最大值,即杯体内液体的最大深度.
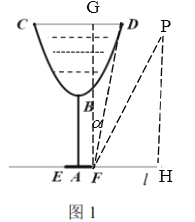
解:如图:作CD的垂线FG,DF绕F旋转后为FP,作PH垂直EF的延长线于H,
由题意可知:FG=21,DG=![]()
![]() ,
,
所以DF=![]() ,
,
所以![]()
所以![]() =
=![]() ,
,
所以![]() =
=![]()
所以PH=FP![]() =
=![]()
![]() =
=![]() ,
,
液面![]() 到平面
到平面![]() 的距离是
的距离是![]() ;
;
如图3,建立直角坐标系,在DG下方的抛物线上任取一点Q,过点Q作y轴的平行线交DG于点P,过点Q作DG的垂线QM,垂足为M,
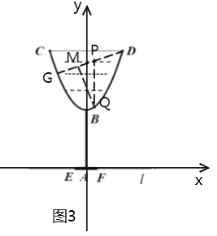
由题意可知DG绕F点顺时针旋转![]() 后与水平方向平行,所以旋转前DG与水平方向的夹角为
后与水平方向平行,所以旋转前DG与水平方向的夹角为![]() ,设直线DG的解析式为y=kx+b,
,设直线DG的解析式为y=kx+b,
由题意可知,点D的坐标为![]() ,
,
![]() ,
,
所以![]() ,
,
设抛物线的解析式为![]() ,经过点D
,经过点D![]() ,
,
所以a=1,
所以![]() ,
,
由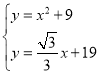 得点G的坐标为
得点G的坐标为![]() ,
,
设Q的坐标为![]() ,点P的坐标为
,点P的坐标为![]() ,
,
所以PQ=![]() =
=![]() ,
,
当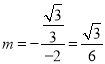 时,PQ有最大值为
时,PQ有最大值为![]() ,
,
又因为![]() =
=![]() ,
,
所以当PQ取最大值时,![]() 有最大值=
有最大值=![]() ,
,
![]() =
=![]() ,
,
又因为![]() =
=![]() ,
,
所以当![]() 有最大值时,QM有最大值,
有最大值时,QM有最大值,
![]() ,
,
所以QM=![]()
所以旋转后杯体内液体的最大深度为![]() ,
,
故答案是:![]() ;
;![]() .
.

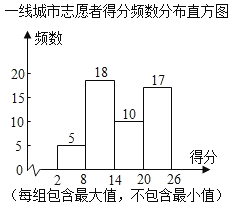
【题目】为了解疫情对精神负荷造成的影响,某机构分别在一线城市和三线城市的志愿者中随机选取了50人参加LES测试,根据志愿者的答题情况计算出LES得分,并对得分进行整理,描述和分析,部分信息如下:
一、三线城市志愿者得分统计表
城市 | 中位数 | 平均数 |
一线城市 | a | 17.6 |
三线城市 | 14 | 17.2 |
注:一线城市在14<x≤20中的得分是:15,15,16,17,17,17,17,18,18,20.
根据以上信息,解答下列问题:
(1)表中a的值为 ;
(2)得分越低反映个体承受的精神压力越小,排名越靠前,在这次调查中,一线城市的志愿者甲和三线城市的志愿者乙的得分均为15分,请判断甲、乙在各自城市选取的志愿者中得分排名谁更靠前,并说明理由;
(3)如果得分超过平均数就需要进行心理干预,请估计一线城市全部2000名志愿者中有多少人需要进行心理干预?