题目内容
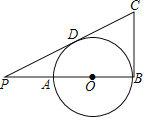
【题目】如图，AB是⊙O的直径，点P在BA的延长线上，PA＝AO，PD与⊙O相切于点D，BC⊥AB交PD的延长线于点C，若⊙O的半径为1，则BC的长是（ ）
A.1.5B.2C.
D.
【答案】D
【解析】
连接OD，根据切线的性质求出∠ODP＝90°，根据勾股定理求出PD，证明BC是⊙O的切线，根据切线长定理得出CD＝BC，再根据勾股定理求出BC即可．
连接OD，如图所示
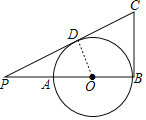
∵PC切⊙O于D
∴∠ODP＝90°
∵⊙O的半径为1，PA＝AO，AB是⊙O的直径
∴PO＝1+1＝2，PB＝1+1+1＝3，OD＝1
∴由勾股定理得：PD＝
∵BC⊥AB，AB过O
∴BC切⊙O于B
∵PC切⊙O于D
∴CD＝BC
设CD＝CB＝x
在Rt△PBC中，由勾股定理得：PC2＝PB2+BC2
即
解得：x＝
即BC＝
故选：D
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
