Question

【题目】已知抛物线y=ax2+bx-3a-5经过点A(2，5)

（1）求出a和b之间的数量关系．

（2）已知抛物线的顶点为D点，直线AD与y轴交于(0，-7)

①求出此时抛物线的解析式；

②点B为y轴上任意一点且在直线y=5和直线y=-13之间，连接BD绕点B逆时针旋转90°，得到线段BC，连接AB、AC，将AB绕点B顺时针旋转90°，得到线段BH．截取BC的中点F和DH的中点G．当点D、点H、点C三点共线时，分别求出点F和点G的坐标．

Answer 1

【答案】（1）a+2b=10；（2）①y= 2x2+4x-11，②G1(，)，F1(，)，G2(，)，F2(，)

【解析】

（1）把点A坐标代入抛物线y=ax2+bx-3a-5即可得到a和b之间的数量关系；

（2）①求出直线AD的解析式，与抛物线y=ax2+bx-3a-5联立方程组，根据直线与抛物线有两个交点，结合韦达定理求出a，b，即可求出解析式；

②作AI⊥y轴于点I，HJ⊥y轴于点J.设B（0，t），根据旋转性质表示粗H、D、C坐标，应含t式子表示直线AD的解析式，根据D、H、C三点共线，把点C坐标代入求出，，分两类讨论，分别求出G、F坐标。

解：（1）把A（2,5）代入y=ax2+bx-3a-5得4a+2b-3a-5=5

∴a+2b=10

∴a和b之间的数量关系是a+2b=10

（2）①设直线AD的解析式为y=kx+c

∵直线AD与y轴交于（0，-7），A（2,5）

∴解得即直线AD的解析式为y=6x-7

联立抛物线y=ax2+bx-3a-5与直线AD：y=6x-7 得

消去y得ax2+（b-6）x-3a+2=0

∵抛物线与直线AD有两个交点

∴由韦达定理可得：xA+xD==，xAxD=

∵A（2,5）∴xA=2即xD=∵xD==

∴=解得a=2∴b== 4

∴此时抛物线的解析式为y= 2x2+4x-11

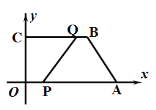
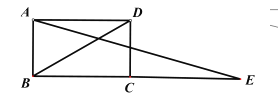
②如图所示：作AI⊥y轴于点I，HJ⊥y轴于点J.设B（0，t）

∵A（2，5），∴AI=2，BJ=5-t

∵AB绕点B顺时针旋转90°，得到线段BH

∴AB=BH，∠ABH=90°，∠AIB=∠BJH=90°

∵∠IAB+∠IBA=90°，∠ABH+∠IBA+∠JBH=180°

∴∠IBA+∠JBH=90°即∠IAB=∠JBH

∴△AJB≌△BJH即AI=BJ=2，BI=IH=5-t

∴H（5-t，t-2）

∵D（-1，-13）∴yB-yD=t+13

同理可得：C（t+13，t-1）

设DH的解析式为y=k1x+b1

∴解得

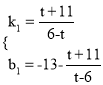
即直线AD的解析式为

∵D、H、C三点共线

∴把C（t+13，t-1）代入得：

整理得2t2+31t+82=0解得，

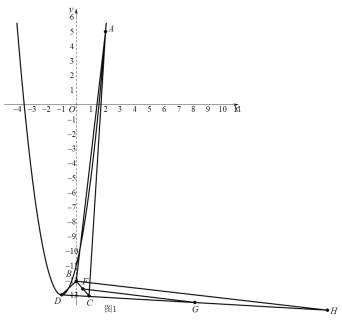
由图可知：①当如图1所示：

此时H（，） ，C（，）

∵点G为DH中点，点F为BC中点

∴G1（，） ，F1（，）

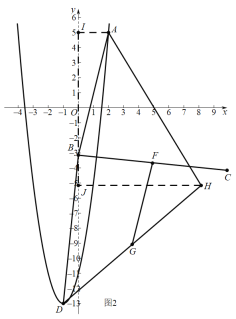
由图可知：当如图2所示：

此时H（，） ，C（，）

∵点G为DH中点，点F为BC中点

∴G2（，） ，F2（，） （14分）

∴综上所述：G1（，） ，F1（，）

G2（，） ，F2（，）。