题目内容
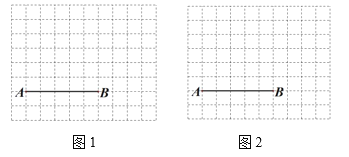
【题目】图1、图2分别是![]() 的网格,网格中每个小正方形的边长均为1,
的网格,网格中每个小正方形的边长均为1,![]() 、
、![]() 两点在小正方形的顶点上,请在图1、图2中各取一点
两点在小正方形的顶点上,请在图1、图2中各取一点![]() (点
(点![]() 必须在小正方形的顶点上),使以
必须在小正方形的顶点上),使以![]() 、
、![]() 、
、![]() 为顶点的三角形分别满足以下要求:
为顶点的三角形分别满足以下要求:
(1)在图1中画一个![]() ,使
,使![]() 是以
是以![]() 为斜边的直角三角形,且
为斜边的直角三角形,且![]() ;
;
(2)在图2中画一个![]() ,使
,使![]() 为等腰三角形,且
为等腰三角形,且![]() ,直接写出
,直接写出![]() 的长度.
的长度.
【答案】(1)画图见解析;(2)画图见解析;AC的长度为![]() 或
或![]() .
.
【解析】
(1)![]() 是以
是以![]() 为斜边的直角三角形,
为斜边的直角三角形,![]() ,则AC=2BC,利用勾股定理求得BC,AC的长度,然后利用格点的特点找点C;
,则AC=2BC,利用勾股定理求得BC,AC的长度,然后利用格点的特点找点C;
(2)![]() 为等腰三角形,且
为等腰三角形,且![]() ,则AB为三角形的腰,则BC=5,结合勾股定理和格点的特征确定点C的位置,然后利用勾股定理求AC的长度.
,则AB为三角形的腰,则BC=5,结合勾股定理和格点的特征确定点C的位置,然后利用勾股定理求AC的长度.
解:(1)∵![]() 是以
是以![]() 为斜边的直角三角形,
为斜边的直角三角形,![]() ,则AC=2BC
,则AC=2BC
∴在Rt△ABC中,![]()
解得![]() ,
,![]()
又∵![]()
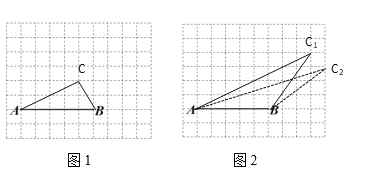
∴如图1,Rt△ABC即为所求;
(2)∵![]() 为等腰三角形,且
为等腰三角形,且![]() ,则AB为三角形的腰,
,则AB为三角形的腰,
∴BC=5
∵![]()
∴如图2,等腰三角形ABC1和等腰三角形ABC2即为所求
此时![]() ,
,![]()
∴AC的长度为:![]() 或
或![]() .
.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目