题目内容
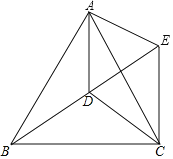
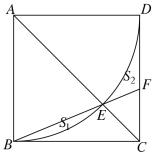
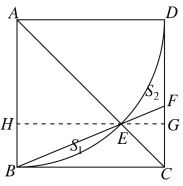
【题目】如图，在正方形ABCD中，以A为圆心，AB为半径作 
，交对角线AC于点E，连结BE并延长交CD于点F，记图中分割部分的面积为S1，S2．则下列对S1与S2的大小关系判断正确的是( )
A.S1>S2B.S1<S2C.S1=S2D.与正方形ABCD的边长有关
【答案】B
【解析】
过E作EH⊥AB，延长HE与CD交于点G，设正方形的边长为a，由题意可知AB=AD=AE=DC=a，利用相似三角形的判定和性质，可证得CE=CF，利用解直角三角形分别求出AC，HE，CF，EG的长，然后根据S1=S扇形BAE-S△ABE ，S2=S△ADC-S扇形BAE-S△CEF，就可求出S1-S2的值，根据其值的大小，可作出判断.
如图，过E作EH⊥AB，延长HE与CD交于点G，
设正方形的边长为a，
由题意可知AB=AD=AE=DC=a，AB∥CD
∴△ABE∽△CFE
∴
，即
∴CE=CF
在Rt△ABC中，AC=
在Rt△AEH中，∠HAE=45°，
∴
∴HE=
∴CE=CF=AC-AE=
在Rt△CEG中，∠ECG=45°，
∴sin∠ECG=
解得
∴S1=S扇形BAE-S△ABE，S2=S△ADC-S扇形BAE-S△CEF
∴S1-S2=S扇形BAE-S△ABE-S△ADC+S扇形BAE+S△CEF
=2S扇形BAE-S△ABE-S△ADC+S△CEF
=S扇形BAD-(S正方形ABCD-S△BEC)+S△CEF
=S扇形BAD-S正方形ABCD+S△BEC+S△CEF
＜0
∴S1＜S2
故选B.
练习册系列答案
阅读快车系列答案
相关题目
