题目内容
【题目】如图,在Rt△ABC中,∠ABC=90°,CD⊥BC,BD与AC相交于点E,AB=9,BC=4,DC=3.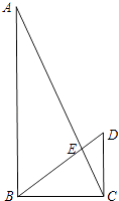
(1)求BE的长度;
(2)求△ABE的面积.
【答案】
(1)解:∵CD⊥BC,
∴∠DCB=90°,
在Rt△BCD中,BC=4,DC=3,
根据勾股定理得:BD= ![]() =5,
=5,
∵AB∥CD,
∴△ABE∽△CDE,
∴DC:AB=DE:BE=3:9=1:3,
又∵BD=5,
∴BE= ![]() BD=
BD= ![]()
(2)解:作EF⊥AB,EH⊥CD,
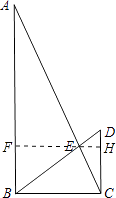
∵△ABE∽△CDE,
∴EF:EH=DC:AB=1:3,
又∵BC=4,
∴FE= ![]() BC=3,EF的长,
BC=3,EF的长,
则S△ABE=AB×EF× ![]() =
= ![]() .
.
【解析】(1)在Rt△BCD中根据勾股定理得出BD的长,根据平行于三角形一边的直线截其它两边的延长线,所截得的三角形与原三角形相似得出△ABE∽△CDE,根据相似三角形对应边成比例得出DC:AB=DE:BE=3:9=1:3,从而得出答案;
(2)作EF⊥AB,EH⊥CD,根据相似三角形对应高的比等于相似比得出EF的长,从而根据三角形的面积公式计算即可。
【考点精析】关于本题考查的相似三角形的判定与性质,需要了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.

练习册系列答案
相关题目